O desvio padrão é a quantidade média de variabilidade no seu conjunto de dados. Ele diz, em média, a que distância cada valor está da média.
Um desvio padrão alto significa que os valores estão geralmente longe da média, enquanto um desvio padrão baixo indica que os valores estão agrupados perto da média.
- O que o desvio padrão lhe diz?
- A regra empírica
- Fórmulas de desvio padrão para populações e amostras
- Desvio-padrão da população
- Qual é a sua pontuação de plágio?
- Passos para o cálculo do desvio padrão
- Passo 1: Encontrar a média
- Passo 2: Encontre o desvio de cada pontuação da média
- Passo 3: Quadrar cada desvio da média
- Passo 4: Encontrar a soma dos quadrados
- Passo 5: Encontre a variância
- Passo 6: Encontrar a raiz quadrada da variância
- Por que o desvio padrão é uma medida útil de variabilidade?
- Perguntas frequentes sobre o desvio padrão
O que o desvio padrão lhe diz?
Desvio padrão é uma medida útil de dispersão para distribuições normais.
Em distribuições normais, os dados são simetricamente distribuídos sem inclinação. A maioria dos valores se agrupa em torno de uma região central, com valores afunilados à medida que se afastam do centro. O desvio padrão diz a você como os dados se espalham do centro da distribuição em média.
Muitas variáveis científicas seguem distribuições normais, incluindo altura, escores de teste padronizados ou índices de satisfação no trabalho. Quando você tem os desvios padrão de diferentes amostras, você pode comparar suas distribuições usando testes estatísticos para fazer inferências sobre as populações maiores de onde vieram.
As médias (M) dos índices são as mesmas para cada grupo – é o valor no eixo x quando a curva está no seu pico. Entretanto, seus desvios padrão (DP) diferem entre si.
O desvio padrão reflete a dispersão da distribuição. A curva com o menor desvio padrão tem um pico alto e uma pequena dispersão, enquanto a curva com o maior desvio padrão é mais plana e difundida.

A regra empírica
O desvio padrão e a média juntos podem dizer onde se encontra a maioria dos valores na sua distribuição se seguirem uma distribuição normal.
A regra empírica, ou a regra 68-95-99.7, diz-lhe onde se encontram os seus valores:
- A ronda 68% das pontuações estão dentro de 2 desvios padrão da média,
- A ronda 95% das pontuações estão dentro de 4 desvios padrão da média,
- A ronda 99.7% das pontuações estão dentro de 6 desvios-padrão da média,
Seguir a regra empírica:
- Rode 68% dos escores estão entre 40 e 60,
- Rode 95% dos escores estão entre 30 e 70.
- Terra 99,7% das pontuações estão entre 20 e 80,


A regra empírica é uma forma rápida de obter uma visão geral dos seus dados e verificar se existem valores anómalos ou extremos que não sigam este padrão.
Para distribuições não normais, o desvio padrão é uma medida menos confiável de variabilidade e deve ser usado em combinação com outras medidas como a faixa ou intervalo interquartil.
Fórmulas de desvio padrão para populações e amostras
Fórmulas diferentes são usadas para calcular os desvios padrão, dependendo se você tem dados de toda uma população ou de uma amostra.
Desvio-padrão da população
Quando você tiver coletado dados de cada membro da população que você está interessado, você pode obter um valor exato para o desvio-padrão da população.
A fórmula do desvio padrão da população tem este aspecto:
| Fórmula | Explicação |
|---|---|
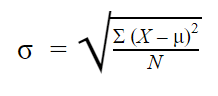 |
|
Desvio padrão da amostra
Quando você coleta dados de uma amostra, o desvio padrão da amostra é usado para fazer estimativas ou inferências sobre o desvio padrão da população.
A fórmula do desvio padrão da amostra tem este aspecto:
| Fórmula | Explicação |
|---|---|
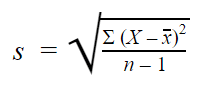 |
|
Com amostras, usamos n – 1 na fórmula porque o uso de n nos daria uma estimativa tendenciosa que subestima consistentemente a variabilidade. O desvio padrão da amostra tenderia a ser inferior ao desvio padrão real da população.
Reduzir a amostra n a n – 1 torna o desvio padrão artificialmente grande, dando-lhe uma estimativa conservadora da variabilidade.
Embora não seja uma estimativa imparcial, é uma estimativa menos enviesada do desvio padrão: é melhor sobrestimar do que subestimar a variabilidade das amostras.
Passos para o cálculo do desvio padrão
O desvio padrão é normalmente calculado automaticamente por qualquer software que você use para sua análise estatística. Mas você também pode calculá-lo manualmente para entender melhor como a fórmula funciona.
Existem seis passos principais para encontrar o desvio padrão à mão. Usaremos um pequeno conjunto de dados de 6 pontuações para caminhar através dos passos.
| Conjunto de dados | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
Passo 1: Encontrar a média
Para encontrar a média, somar todas as pontuações e depois dividi-las pelo número de pontuações.
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50
Passo 2: Encontre o desvio de cada pontuação da média
Subtraia a média de cada pontuação para obter os desvios da média.
Desde x̅ = 50, aqui retiramos 50 de cada pontuação.
| Partitura | Desvio da média |
|---|---|
| 46 | 46 – 50 = -4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
Passo 3: Quadrar cada desvio da média
Multiplicar cada desvio da média por si só. Isto resultará em números positivos.
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81
Passo 4: Encontrar a soma dos quadrados
Adicionar todos os desvios ao quadrado. Isto é chamado soma dos quadrados.
16 + 361 + 324 + 100 + 4 + 81 = 886
Passo 5: Encontre a variância
Divida a soma dos quadrados por n – 1 (para uma amostra) ou N (para uma população) – esta é a variância.
Desde que estamos trabalhando com um tamanho de amostra de 6, usaremos n – 1, onde n = 6,
886 ÷ (6 – 1) = 886 ÷ 5 = 177.2
Passo 6: Encontrar a raiz quadrada da variância
Para encontrar o desvio padrão, tomamos a raiz quadrada da variância.
√177.2 = 13.31
>De aprender que SD = 13.31, podemos dizer que cada pontuação se desvia da média em 13,31 pontos em média.
Por que o desvio padrão é uma medida útil de variabilidade?
Embora existam formas mais simples de calcular a variabilidade, a fórmula do desvio padrão pesa mais desigualmente as amostras espalhadas do que as amostras espalhadas uniformemente. Um desvio padrão maior diz-lhe que a distribuição não só é mais distribuída, mas também mais desigualmente distribuída.
Isto significa que lhe dá uma melhor ideia da variabilidade dos seus dados do que medidas mais simples, como o desvio médio absoluto (DMA).
O DMA é semelhante ao desvio padrão, mas mais fácil de calcular. Primeiro, você expressa cada desvio da média em valores absolutos, convertendo-os em números positivos (por exemplo, -3 torna-se 3). Depois, você calcula a média desses desvios absolutos.
Não é necessário calcular quadrados ou raízes quadradas de números para o DMA, como o desvio padrão. No entanto, por essa razão, dá-lhe uma medida menos precisa da variabilidade.
Vamos tirar duas amostras com a mesma tendência central mas com quantidades diferentes de variabilidade. A amostra B é mais variável do que a amostra A.
| Valores | Mean | Desvio absoluto do comportamento | Desvio padrão | ||
|---|---|---|---|---|---|
| Amostra A | 66, 30, 40, 64 | 50 | 15 | 17.8 | |
| Amostra B | 51, 21, 79, 49 | 50 | 15 | 23.7 |
Para amostras com desvios médios iguais à média, o DMA não consegue diferenciar os níveis de espalhamento. O desvio padrão é mais preciso: é maior para a amostra com maior variabilidade nos desvios da média.
Ao quadrar as diferenças em relação à média, o desvio padrão reflete a dispersão desigual de forma mais precisa. Este passo pesa mais os desvios extremos do que os pequenos desvios.
No entanto, isto também torna o desvio padrão sensível a outliers.
Perguntas frequentes sobre o desvio padrão
A variabilidade é mais comumente medida com a seguinte estatística descritiva:
- Gama: a diferença entre os valores mais altos e mais baixos
- Gama interquartílica: o intervalo da metade média de uma distribuição
- Desvio padrão: distância média da média
- Variância: distância média ao quadrado da média
O desvio padrão é a quantidade média de variabilidade no seu conjunto de dados. Ele diz-lhe, em média, a que distância está cada pontuação da média.
Em distribuições normais, um desvio padrão alto significa que os valores estão geralmente longe da média, enquanto um desvio padrão baixo indica que os valores estão agrupados perto da média.
Em uma distribuição normal, os dados são simetricamente distribuídos sem inclinação. A maioria dos valores se agrupa em torno de uma região central, com valores afunilados à medida que se afastam do centro.
As medidas de tendência central (média, modo e mediana) são exatamente as mesmas em uma distribuição normal.
A regra empírica, ou a regra 68-95-99.7, diz-lhe onde se encontra a maioria dos valores numa distribuição normal:
- Around 68% dos valores estão dentro de 1 desvio padrão da média.
- Around 95% dos valores estão dentro de 2 desvios padrão da média.
- Around 99.7% dos valores estão dentro de 3 desvios padrão da média.
A regra empírica é uma forma rápida de obter uma visão geral dos seus dados e verificar se existem valores anómalos ou extremos que não seguem este padrão.
Variância é o desvio médio ao quadrado da média, enquanto o desvio padrão é a raiz quadrada deste número. Ambas as medidas refletem variabilidade em uma distribuição, mas suas unidades diferem:
- Desvio padrão é expresso nas mesmas unidades que os valores originais (por exemplo, minutos ou metros).
- Variância é expressa em unidades muito maiores (por exemplo, metros quadrados).
Embora as unidades de variância sejam mais difíceis de entender intuitivamente, a variância é importante em testes estatísticos.
