Édito Mesopotâmico
O período 2700-2300 a.C. viu o primeiro aparecimento do ábaco sumério, uma tabela de colunas sucessivas que delimitou as sucessivas ordens de magnitude do seu sistema de números sexagesimais.
Alguns estudiosos apontam para um personagem em cuneiforme babilônico que pode ter sido derivado de uma representação do ábaco. É a crença de estudiosos babilônicos antigos como Carruccio que os babilônios antigos “podem ter usado o ábaco para as operações de adição e subtração; no entanto, este dispositivo primitivo provou ser difícil de usar para cálculos mais complexos”.
EgyptianEdit
O uso do ábaco no Antigo Egipto é mencionado pelo historiador grego Heródoto, que escreve que os egípcios manipularam os seixos da direita para a esquerda, em direcção oposta ao método grego da esquerda para a direita. Arqueólogos encontraram discos antigos de vários tamanhos que se pensa terem sido usados como contadores. No entanto, as representações de parede deste instrumento não foram descobertas.
PersianEdit
Durante o Império Aqueménida, por volta de 600 a.C. os Persas começaram a usar o ábaco pela primeira vez. Sob os impérios Parthian, Sassanian e Iranian, os estudiosos concentraram-se na troca de conhecimento e invenções com os países ao seu redor – Índia, China, e Império Romano, quando se pensa ter sido exportado para outros países.
GreekEdit
>
As primeiras provas arqueológicas para o uso do ábaco grego datam do século V aC. Também Demóstenes (384 a.C.-322 a.C.) falou da necessidade de usar seixos para cálculos demasiado difíceis para a sua cabeça. Uma peça de Alexis do século IV aC menciona um ábaco e seixos para contabilidade, e tanto Diógenes como Políbio mencionam homens que às vezes representam mais e às vezes menos, como os seixos de um ábaco. O ábaco grego era uma mesa de madeira ou mármore, pré-estabelecida com pequenos contadores em madeira ou metal para cálculos matemáticos. Este ábaco grego foi usado na Pérsia Aqueménida, na civilização etrusca, na Roma Antiga e, até à Revolução Francesa, no mundo cristão ocidental.
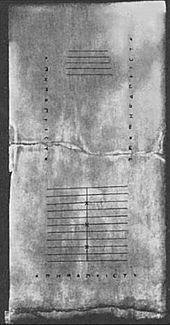
Uma tábua encontrada na ilha grega Salamis em 1846 d.C. (a Tábua de Salamis), data de 300 a.C., tornando-a a mais antiga tábua de contagem descoberta até agora. É uma placa de mármore branco de 149 cm de comprimento, 75 cm de largura e 4,5 cm de espessura, sobre a qual se encontram 5 grupos de marcações. No centro da tábua está um conjunto de 5 linhas paralelas igualmente divididas por uma linha vertical, com um semicírculo na intersecção da linha horizontal mais inferior e da linha vertical única. Abaixo destas linhas há um amplo espaço com uma fenda horizontal que a divide. Abaixo desta fenda há outro grupo de onze linhas paralelas, novamente divididas em duas secções por uma linha perpendicular a elas, mas com o semicírculo no topo da intersecção; a terceira, sexta e nona destas linhas estão marcadas com uma cruz onde se intersectam com a linha vertical. Também a partir deste período o vaso Darius Vase foi desenterrado em 1851. Ele foi coberto com figuras incluindo um “tesoureiro” segurando uma pastilha de cera em uma mão enquanto manipulava contadores em uma mesa com a outra.
ChineseEdit

>
| Abacus | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chinesa tradicional | 算盤 | |||||||||||||||
| Chinês simplificado | 算盘 | |||||||||||||||
| Literal significado | “bandeja de cálculo” | |||||||||||||||
| Transcrições | Mandarim-padrão | Hanyu Pinyin | IPA | Yue: Cantonês | Romanização Yale | Jyutping | IPA | Southern Min | Hokkien POJ | Tâi-lô | ||||||
A documentação escrita mais antiga conhecida do ábaco chinês data do século II a.C.
O ábaco chinês, conhecido como o suanpan (算盘/算盘, aceso “tabuleiro de cálculo”), tem tipicamente 20 cm (8 pol.) de altura e vem em várias larguras, dependendo do operador. Normalmente tem mais de sete varas. Há duas contas em cada vara no convés superior e cinco contas em cada uma na parte inferior. Os grânulos são normalmente arredondados e feitos de madeira dura. Os grânulos são contados movendo-os para cima ou para baixo em direcção à viga; os grânulos movidos em direcção à viga são contados, enquanto os que se afastam dela não o são. Uma das contas de cima é 5, enquanto uma das contas de baixo é 1. Cada vara tem um número debaixo dela, mostrando o valor do lugar. O suanpan pode ser reposto na posição inicial instantaneamente por um movimento rápido ao longo do eixo horizontal para girar todas as contas para longe da viga horizontal no centro.
O protótipo do ábaco chinês apareceu durante a Dinastia Han, e as contas são ovais. A Dinastia da Canção e anteriormente utilizava o tipo 1:4 ou ábaco de quatro contas semelhante ao ábaco moderno, incluindo a forma das contas comumente conhecidas como ábaco estilo japonês.
No início da Dinastia Ming, o ábaco começou a aparecer na forma de ábaco 1:5. O andar superior tinha uma conta e o inferior tinha cinco contas.
No final da Dinastia Ming, os estilos de ábaco apareceram sob a forma de 2:5. O convés superior tinha duas contas, e o inferior tinha cinco contas.
Várias técnicas de cálculo foram concebidas para Suanpan permitindo cálculos eficientes. Existem atualmente escolas ensinando aos alunos como usá-lo.
No longo pergaminho ao longo do rio Durante o Festival de Qingming pintado por Zhang Zeduan durante a dinastia Song (960-1297), um suanpan é claramente visível ao lado de um livro de contas e prescrições médicas no balcão de um boticário (Feibao).
A semelhança do ábaco romano com o chinês sugere que um poderia ter inspirado o outro, pois há algumas evidências de uma relação comercial entre o Império Romano e a China. Entretanto, nenhuma conexão direta pode ser demonstrada, e a similaridade dos ábacos pode ser coincidente, ambos em última instância surgindo da contagem com cinco dedos por mão. Onde o modelo romano (como a maioria dos coreanos modernos e japoneses) tem 4 mais 1 conta por casa decimal, o suanpano padrão tem 5 mais 2. A propósito, isto permite o uso com um sistema de numeração hexadecimal (ou qualquer base até 18) que pode ter sido usado para medidas tradicionais chinesas de peso. (Em vez de correr em fios como nos modelos chinês, coreano e japonês, as contas do modelo romano correm em ranhuras, presumivelmente fazendo cálculos aritméticos muito mais lentos.
Outra fonte possível do suanpan é o chinês de varetas de contagem, que funcionava com um sistema decimal, mas faltava o conceito de zero como um suporte de posição. O zero foi provavelmente introduzido aos chineses na dinastia Tang (618-907) quando viagens no Oceano Índico e no Oriente Médio teriam proporcionado contato direto com a Índia, permitindo-lhes adquirir o conceito de zero e o ponto decimal de comerciantes e matemáticos indianos.
RomanEdit

O método normal de cálculo na Roma antiga, como na Grécia, era movendo os contadores em uma mesa lisa. Originalmente eram usados seixos (cálculos). Mais tarde, e na Europa medieval, os jetons eram fabricados. Linhas marcadas indicavam unidades, cinco, dez, etc., como no sistema de numerais romanos. Este sistema de “contra casting” continuou no final do império romano e na Europa medieval, e persistiu em uso limitado no século XIX. Devido à reintrodução do ábaco pelo Papa Silvestre II com modificações, tornou-se amplamente utilizado na Europa mais uma vez durante o século XI. Este ábaco usava contas em arames, ao contrário das tradicionais placas de contagem romanas, o que significava que o ábaco podia ser utilizado muito mais rapidamente.
Escrita no século I a.C., Horácio refere-se ao ábaco de cera, uma tábua coberta com uma fina camada de cera preta na qual colunas e figuras eram inscritas usando um estilete.
Um exemplo de evidência arqueológica do ábaco romano, mostrado aqui na reconstrução, data do século I d.C. Tem oito ranhuras longas contendo até cinco contas em cada uma e oito ranhuras mais curtas tendo uma ou nenhuma conta em cada uma. A ranhura marcada I indica unidades, X dezenas, e assim por diante até milhões. As contas nos sulcos mais curtos denotam cinco unidades, cinco dezenas etc., essencialmente num sistema bi-quinário codificado decimal, relacionado com os numerais romanos. As ranhuras curtas à direita podem ter sido usadas para marcar “onças” romanas (ou seja, fracções).
IndianEdit
O Abhidharmakośabhāṣya de Vasubandhu (316-396), um trabalho sânscrito sobre filosofia budista, diz que o filósofo Vasumitra do segundo século CE disse que “colocar um pavio (sânscrito vartikā) no número um (ekāṅka) significa que é um, enquanto colocar o pavio no número cem significa que é chamado de cem, e no número mil significa que é mil”. Não está claro exatamente o que este arranjo pode ter sido. Por volta do século V, os escriturários indianos já estavam encontrando novas maneiras de registrar o conteúdo do Ábaco. Textos hindus usavam o termo śūnya (zero) para indicar a coluna vazia no ábaco.
JapaneseEdit

>
Em japonês, o ábaco é chamado de soroban (算盤, そろばん, aceso “Counting tray”), importado da China no século XIV. Estava provavelmente em uso pela classe trabalhadora um século ou mais antes do início da classe dominante, pois a estrutura de classes não permitia que os dispositivos usados pela classe inferior fossem adotados ou usados pela classe dominante. O 1/4 ábaco, que remove o segundo e quinto ábaco raramente usado tornou-se popular na década de 1940.
O ábaco japonês de hoje é um tipo 1:4, o ábaco de quatro esferas foi introduzido da China na era Muromachi. Ele adota a forma de uma conta no convés superior e quatro contas inferiores. A conta superior no convés superior era igual a cinco e a inferior é igual a um como o ábaco chinês ou coreano, e o número decimal pode ser expresso, de modo que o ábaco é projetado como um ábaco de quatro ábacos. Os grânulos têm sempre a forma de um diamante. A divisão do quociente é geralmente usada em vez do método de divisão; ao mesmo tempo, a fim de fazer a multiplicação e os dígitos de divisão usam consistentemente a multiplicação de divisão. Mais tarde, o Japão tinha um ábaco 3:5 chamado 天三算盤, que agora é a coleção Ize Rongji da Vila Shansi na cidade de Yamagata. Havia também ábaco do tipo 2:5.
Com o ábaco de quatro contas espalhadas, também é comum usar ábaco japonês ao redor do mundo. Há também ábaco japonês melhorado em vários lugares. Um dos ábacos japoneses feitos na China é um ábaco de esferas de plástico com estrutura de alumínio. O arquivo está ao lado dos quatro grânulos, e o botão “clearing”, pressione o botão clearing, coloque imediatamente o grânulo superior na posição superior, o grânulo inferior é discado para a posição inferior, imediatamente clear, fácil de usar.
O ábaco ainda hoje é fabricado no Japão, mesmo com a proliferação, praticidade e acessibilidade de calculadoras eletrônicas de bolso. O uso do soroban ainda é ensinado nas escolas primárias japonesas como parte da matemática, principalmente como uma ajuda para o cálculo mental mais rápido. Usando imagens visuais de um soroban, pode-se chegar à resposta ao mesmo tempo que, ou até mais rápido que, é possível com um instrumento físico.
KoreanEdit
O ábaco chinês migrou da China para a Coreia por volta de 1400 DC. Os coreanos chamam-lhe jupan (주판), supan (수판) ou jusan (주산). Os quatro ábacos de contas( 1:4 ) foram introduzidos na Coreia Dinastia Goryeo da China durante a Dinastia Song, mais tarde os cinco ábacos de contas (5:1) foram introduzidos no coreano da China durante a Dinastia Ming.
Native AmericanEdit


>
Algumas fontes mencionam o uso de um ábaco chamado nepohualtzintzin na cultura Azteca antiga. Este ábaco mesoamericano usava um sistema de base de 5 dígitos – 20. A palavra Nepōhualtzintzin vem de Nahuatl e é formada pelas raízes; Ne – pessoal -; pōhual ou pōhualli – a conta -; e tzintzin – pequenos elementos similares. O seu significado completo foi tomado como: contar com pequenos elementos semelhantes por alguém. Seu uso foi ensinado no Calmecac ao temalpouhqueh , que eram estudantes dedicados a levar os relatos dos céus, desde a infância.
O Nepōhualtzintzin foi dividido em duas partes principais separadas por uma barra ou cordão intermediário. Na parte esquerda havia quatro contas, que na primeira linha têm valores unitários (1, 2, 3, e 4), e no lado direito há três contas com valores de 5, 10, e 15 respectivamente. Para conhecer o valor das respectivas contas das linhas superiores, basta multiplicar por 20 (por cada linha), o valor da conta correspondente na primeira linha.
Junto, havia 13 linhas com 7 contas em cada uma, que compunham 91 contas em cada Nepōhualtzintzin. Este era um número básico para entender, 7 vezes 13, uma estreita relação concebida entre os fenómenos naturais, o submundo e os ciclos dos céus. Um Nepōhualtzintzin (91) representa o número de dias que uma estação do ano dura, dois Nepōhualtzitzin (182) é o número de dias do ciclo do milho, desde sua semeadura até sua colheita, três Nepōhualtzintzin (273) é o número de dias de gestação de um bebê, e quatro Nepōhualtzintzin (364) completaram um ciclo e aproximadamente um ano (11/4 dias a menos). Quando traduzido para a aritmética moderna do computador, o Nepōhualtzintzin atingiu a classificação de 10 a 18 em ponto flutuante, o que calculou quantidades estelares e infinitesimais com precisão absoluta, significando que nenhum arredondamento foi permitido.
A redescoberta do Nepōhualtzintzin foi devida ao engenheiro mexicano David Esparza Hidalgo, que em suas andanças pelo México encontrou diversas gravuras e pinturas deste instrumento e reconstruiu várias delas feitas em ouro, jade, incrustações de concha, etc. Também foi encontrado muito antigo Nepōhualtzintzin atribuído à cultura olmeca, e até algumas pulseiras de origem maia, bem como uma diversidade de formas e materiais em outras culturas.
George I. Sanchez, “Aritmética em Maya”, Austin-Texas, 1961 encontrou outra base 5, base 4 ábaco na Península de Yucatán que também computava dados de calendário. Este era um ábaco de dedos, por um lado foram utilizados 0, 1, 2, 3 e 4; e por outro lado foram utilizados 0, 1, 2 e 3. Observe o uso de zero no início e no final dos dois ciclos. Sanchez trabalhou com Sylvanus Morley, um notável maia.
O quipu dos Incas era um sistema de cordas com nós coloridos usado para registrar dados numéricos, como varetas de totalização avançada – mas não usado para realizar cálculos. Os cálculos eram feitos usando um yupana (Quechua para “ferramenta de contagem”; ver figura) que ainda estava em uso após a conquista do Peru. O princípio de trabalho de um yupana é desconhecido, mas em 2001 uma explicação da base matemática destes instrumentos foi proposta pelo matemático italiano Nicolino De Pasquale. Comparando a forma de vários yupanas, os pesquisadores descobriram que os cálculos foram baseados usando a seqüência de Fibonacci 1, 1, 2, 3, 5 e potências de 10, 20 e 40 como valores de lugar para os diferentes campos no instrumento. Usando a seqüência de Fibonacci manteria o número de grãos dentro de qualquer campo em um mínimo.
RussianEdit

O ábaco russo, o schoty (Russo: счёты, plural de russo: счёт, contando), geralmente tem um único deck inclinado, com dez contas em cada fio (exceto um fio, geralmente posicionado perto do usuário, com quatro contas para frações de um quarto de rúbrica). Os modelos mais antigos têm outro fio de 4 esferas para quartos de fios, que foram cunhadas até 1916. O ábaco russo é frequentemente usado verticalmente, com cada fio da esquerda para a direita como linhas em um livro. Os fios são normalmente curvados para cima no centro, para manter as contas presas a um dos dois lados. É limpo quando todos os grânulos são movidos para a direita. Durante a manipulação, os grânulos são movidos para a esquerda. Para facilitar a visualização, as 2 contas centrais em cada fio (a 5ª e 6ª contas) são geralmente de uma cor diferente das outras oito contas. Da mesma forma, o terço esquerdo dos milhares de fios (e o milhão de fios, se presente) pode ter uma cor diferente.
Como um dispositivo simples, barato e confiável, o ábaco russo estava em uso em todas as lojas e mercados da antiga União Soviética, e o uso dele foi ensinado na maioria das escolas até os anos 90. Mesmo a invenção da calculadora mecânica de 1874, o arithmómetro Odhner, não os tinha substituído na Rússia; segundo Yakov Perelman, mesmo na sua época, alguns homens de negócios que tentavam importar tais dispositivos para o Império Russo eram conhecidos por desistirem e saírem desesperados depois de lhes ter sido mostrado o trabalho de um hábil operador de ábaco. Da mesma forma, a produção em massa de aritmômetros Felix desde 1924 não reduziu significativamente o seu uso na União Soviética. O ábaco russo começou a perder popularidade somente depois que a produção em massa de microcalculadores tinha começado na União Soviética em 1974. Hoje é considerado como um arcaísmo e substituído pela calculadora manual.
O ábaco russo foi trazido à França por volta de 1820 pelo matemático Jean-Victor Poncelet, que serviu no exército de Napoleão e tinha sido prisioneiro de guerra na Rússia. O ábaco tinha caído fora de uso na Europa Ocidental no século XVI com o aumento da notação decimal e métodos algorítmicos. Para os contemporâneos franceses de Poncelet, era algo novo. Poncelet usou-o, não para nenhuma finalidade aplicada, mas como um auxílio ao ensino e à demonstração. Os turcos e o povo armênio também usaram abusos semelhantes aos do schoty russo. Foi nomeado coulba pelos turcos e corebe pelos armênios.