V této lekci si ukážeme jednoduchou strategii řešení následující úlohy: jak zjistit obsah rovnoramenného trojúhelníku.
Vyzkoušíme si v praxi řadu vlastností, které jsme si dosud dokázali, v následující geometrické úloze:
Úloha
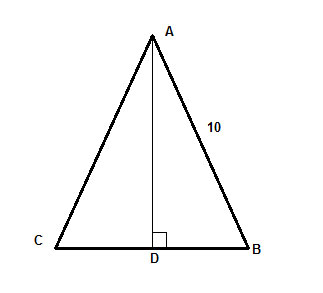
V rovnoramenném trojúhelníku ΔABC s délkou ramene 10 je výška k základně rovna dvěma třetinám základny. Zjistěte obsah trojúhelníku.
Strategie
Pro řešení této úlohy budeme postupovat zpětně od toho, co potřebujeme.
Potřebujeme zjistit obsah trojúhelníku, který, jak víme, je dán vzorcem (základna krát výška)/2.
Problémem je, že neznáme ani délku základny, ani výšku. Je nám však dán vztah mezi nimi, což je nápověda k tomu, co musíme udělat. Nazvěme délku podstavy, BC, x.
Pak víme, že výška, AD, je 2x/3, jak je uvedeno v úloze.
Odpověď, kterou hledáme, je tedy (podstava krát výška)/2, neboli x krát 2x/3, děleno dvěma.
Ale jak zjistíme x? V úloze jsme dostali dvě další věci, které jsme zatím nepoužili – délku ramene (10) a skutečnost, že se jedná o rovnoramenný trojúhelník. Tyto dvě věci pravděpodobně budeme muset použít k vyřešení úlohy.
Zopakujme si vlastnosti rovnoramenných trojúhelníků. Jednou z věcí, která by nás měla okamžitě napadnout, je, že jak jsme si ukázali, v rovnoramenném trojúhelníku výška k základně protíná základnu, takže CD=DB=x/2.
Nakonec AD je výška, což znamená, že úhel ∠ADC je pravý úhel a máme pravoúhlý trojúhelník ΔADC, jehož přeponu známe (10) a můžeme ji použít k nalezení ramen pomocí Pythagorovy věty, c2 =a2+b2,
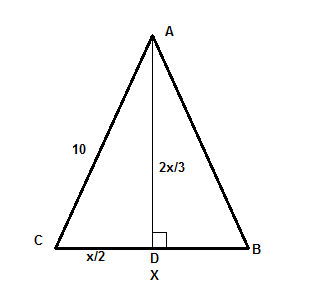
kde c= 10 , a = x/2 a b=2x/3 . A máme hotovo, zbytek je jen algebraické řešení pro x.
Důkaz: Plocha rovnoramenného trojúhelníku
(1) ΔADC je pravoúhlý trojúhelník //dáno, protože AD je výška k základně
(2) AC2 =CD2 + AD2 //Pythagorova věta
(3) AC= 10 //dáno
(4) CB = x
(5) CD = x/2 //výška k základně v rovnoramenném trojúhelníku protíná základnu
(6) AD = 2x/3 //dáno
(7) 102 = (x/2)2 + (2x/3)2 //doplníme do (2)
(8) 100 = x2/4+4×2/9 /zjednodušíme
(9) 100*36 = 9×2 +16×2 //obě strany vynásobíme 36
(10) 100*36 = 25×2 //sebereme podobné výrazy