V moderní době zvuku se nemůžete hnout z místa při zmínce o „Hi-Res“ a 24bitové „studiové kvalitě“ hudby. Pokud jste si nevšimli tohoto trendu ve špičkových chytrých telefonech – Bluetooth kodeku LDAC od Sony – a streamovacích službách jako Tidal, pak byste opravdu měli začít více číst tento web.
Slib je jednoduchý – vynikající kvalita poslechu díky většímu množství dat, alias bitové hloubce. To je 24 bitů digitálních jedniček a nul oproti mizerné 16bitové kocovině z éry CD. Za tyto kvalitnější produkty a služby si samozřejmě budete muset připlatit, ale více bitů je určitě lepší, že?“
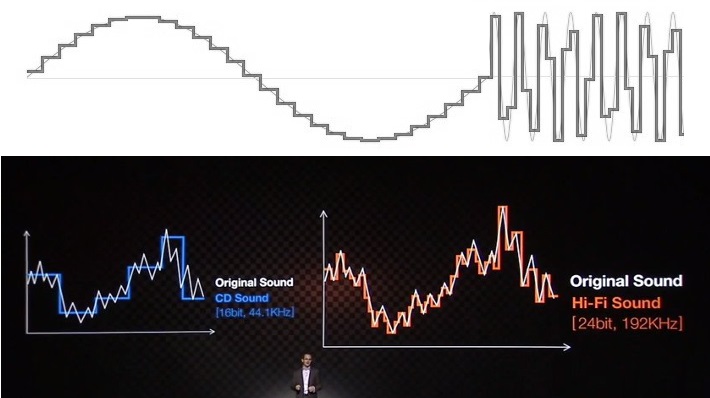
„Low res“ zvuk se často předvádí jako schodovitý průběh. Takto vzorkování zvuku nefunguje a není to to, jak vypadá zvuk vycházející ze zařízení.
Ne nutně. Potřeba stále vyšších a vyšších bitových hloubek není založena na vědecké realitě, ale spíše na překrucování pravdy a využívání nedostatečného povědomí spotřebitelů o vědě o zvuku. V konečném důsledku mají společnosti, které uvádějí na trh 24bitový zvuk, mnohem větší zisk než vy z vyšší kvality přehrávání.
Bitová hloubka a kvalita zvuku:
Aby naznačily, že 24bitový zvuk je nutností, společnosti (a příliš mnoho dalších, kteří se snaží toto téma vysvětlit) se ohánějí velmi známým schodištěm kvality zvuku do nebe. Na 16bitovém příkladu je vždy vidět hrbolatá, trhaná reprodukce sinusového nebo jiného signálu, zatímco 24bitový ekvivalent vypadá krásně hladce a s vyšším rozlišením. Je to jednoduchá vizuální pomůcka, která však spoléhá na neznalost tématu a vědy a vede spotřebitele k nesprávným závěrům.
Než mi někdo ukousne hlavu, technicky vzato tyto příklady schodů skutečně poněkud přesně zobrazují zvuk v digitální oblasti. Nicméně kmenový graf/lollipop chart je přesnější grafické znázornění vizuálního vzorkování zvuku než tyto schodišťové kroky. Přemýšlejte o tom takto – vzorek obsahuje amplitudu ve zcela konkrétním časovém okamžiku, nikoli amplitudu drženou po určitou dobu.

Používání schodišťových grafů je záměrně zavádějící, když kmenové grafy poskytují přesnější zobrazení digitálního zvuku. Tyto dva grafy vykreslují stejné datové body, ale schodišťový graf se zdá být mnohem méně přesný.
Je však správné, že analogově-digitální převodník (ADC) musí vměstnat nekonečný analogový zvukový signál do konečného počtu bitů. Bit, který spadá mezi dvě úrovně, musí být zaokrouhlen na nejbližší aproximaci, což je známo jako kvantizační chyba nebo kvantizační šum. (Zapamatujte si to, protože se k tomu ještě vrátíme.)
Pokud se však podíváte na zvukový výstup jakéhokoli zvukového digitálně analogového převodníku (D/A převodníku) postaveného v tomto století (a pravděpodobně i dávno předtím), žádné schody nezaznamenáte. A to ani v případě, že na výstupu je 8bitový signál. Co to tedy znamená?“

8bitový, 10kHz sinusový výstup zachycený z levného smartphonu Pixel 3a. Vidíme nějaký šum, ale žádné znatelné schodovité kroky, které tak často prezentují zvukové společnosti.
Předně, to, co tyto schodovité diagramy popisují, pokud je aplikujeme na zvukový výstup, je něco, čemu se říká převodník D/A s nulovým řádem. Jedná se o velmi jednoduchou a levnou technologii D/A převodníku, kde se signál přepíná mezi různými úrovněmi při každém novém vzorku, čímž se získá výstup. Tato technologie se nepoužívá v žádných profesionálních ani alespoň trochu slušných spotřebitelských audio produktech. Možná ji najdete v mikrokontroléru za 5 dolarů, ale určitě ne nikde jinde. Zkreslení zvukových výstupů tímto způsobem naznačuje zkreslený, nepřesný průběh, ale to není to, co dostáváte.

Ve skutečnosti je výstupem moderního převodníku ∆Σ převzorkovaný 1bitový signál PDM (vpravo), nikoliv signál s nulovým držením (vlevo). Ten po filtraci vytváří analogový výstup s nižším šumem.
Audio-grade ADC a D/A převodníky jsou převážně založeny na modulaci delta-sigma (∆Σ). Součásti tohoto kalibru zahrnují interpolaci a převzorkování, tvarování šumu a filtrování pro vyhlazení a snížení šumu. Delta-sigma převodníky převádějí zvukové vzorky na 1bitový proud (pulzní hustotní modulace) s velmi vysokou vzorkovací frekvencí. Po filtraci vzniká hladký výstupní signál se šumem vytlačeným daleko od slyšitelných frekvencí.
Zjednodušeně řečeno: moderní převodníky D/A nevytvářejí na výstupu hrubě vypadající zubaté zvukové vzorky – vytvářejí bitový proud, který je filtrován šumem na velmi přesný a hladký výstup. Tato schodovitá vizualizace je špatná kvůli něčemu, čemu se říká „kvantizační šum“.
Pochopení kvantizačního šumu
V každém konečném systému dochází k zaokrouhlovacím chybám. Je pravda, že 24bitový ADC nebo D/A převodník bude mít menší zaokrouhlovací chybu než 16bitový ekvivalent, ale co to vlastně znamená? A co je důležitější, co vlastně slyšíme? Je to zkreslení nebo fuzz, jsou detaily navždy ztraceny?“
Vlastně je to od obojího trochu, podle toho, zda se pohybujete v digitální nebo analogové sféře. Klíčovým konceptem pro pochopení obojího je však pochopení šumové podlahy a toho, jak se zlepšuje s rostoucí bitovou hloubkou. Abychom si to ukázali, ustupme od 16 a 24 bitů a podívejme se na příklady s velmi malou bitovou hloubkou.
Rozdíl mezi 16 a 24bitovou hloubkou není v přesnosti tvaru křivky, ale v dostupné hranici, než náš signál naruší digitální šum.
Na níže uvedeném příkladu je poměrně dost věcí, které je třeba zkontrolovat, takže nejprve krátké vysvětlení, na co se díváme. V horních grafech máme náš vstupní (modrý) a kvantizovaný (oranžový) průběh s bitovou hloubkou 2, 4 a 8 bitů. Do našeho signálu jsme také přidali malé množství šumu, abychom lépe simulovali skutečný svět. V dolní části máme graf kvantizační chyby neboli zaokrouhlovacího šumu, který se vypočítá odečtením kvantizovaného signálu od vstupního signálu.

Kvantizační šum se zvyšuje tím více, čím menší je bitová hloubka, a to díky zaokrouhlovacím chybám.
Zvětšováním bitové hloubky se kvantizovaný signál zjevně lépe přizpůsobuje vstupnímu signálu. To však není to, co je důležité, pozorujte mnohem větší chybu/šum signálu pro nižší bitové hloubky. Kvantovaný signál neodstranil data z našeho vstupu, ale ve skutečnosti přidal tento chybový signál. Aditivní syntéza nám říká, že signál lze reprodukovat součtem jakýchkoli dvou jiných signálů, včetně signálů mimo fázi, které fungují jako odečítání. Takto funguje potlačení šumu. Takže tyto zaokrouhlovací chyby zavádějí nový šumový signál.
To není jen teoretické, ve zvukových souborech s nižší bitovou hloubkou můžete skutečně slyšet stále více šumu. Abyste pochopili proč, prozkoumejte, co se děje v příkladu s 2bitovou hloubkou u velmi malých signálů, například před 0,2 sekundy. Pro zvětšený graf klikněte sem. Velmi malé změny vstupního signálu způsobují velké změny v kvantizované verzi. Jedná se o zaokrouhlovací chybu v akci, která má za následek zesílení šumu malých signálů. Takže ještě jednou, šum se stává hlasitějším s klesající bitovou hloubkou.
Kvantizace neodstraňuje data z našeho vstupu, ale ve skutečnosti přidává šumový chybový signál.
Přemýšlejte o tom i obráceně: není možné zachytit signál menší než velikost kvantizačního kroku – paradoxně známého jako nejméně významný bit. Malé změny signálu musí přeskočit na nejbližší kvantizační stupeň. Větší bitové hloubky mají menší kvantizační kroky, a tedy i menší úroveň zesílení šumu.
Nejdůležitější je však uvědomit si, že amplituda kvantizačního šumu zůstává konzistentní bez ohledu na amplitudu vstupních signálů. To dokazuje, že šum se vyskytuje na všech různých kvantizačních úrovních, takže pro každou danou bitovou hloubku existuje konzistentní úroveň šumu. Větší bitové hloubky produkují méně šumu. O rozdílech mezi 16 a 24 bitovými hloubkami bychom proto neměli uvažovat jako o přesnosti tvaru křivky, ale jako o dostupné hranici, než náš signál naruší digitální šum.
Bitová hloubka je především o šumu
Když už mluvíme o bitové hloubce z hlediska šumu, vraťme se ještě jednou k našemu výše uvedenému grafu. Všimněte si, jak 8bitový příklad vypadá jako téměř dokonalá shoda s naším zašuměným vstupním signálem. Je to proto, že jeho 8bitové rozlišení skutečně stačí k zachycení úrovně šumu na pozadí. Jinými slovy: velikost kvantizačního kroku je menší než amplituda šumu, neboli poměr signál/šum (SNR) je lepší než úroveň šumu pozadí.
Rovnice 20log(2n), kde n je bitová hloubka, nám udává SNR. U 8bitového signálu je SNR 48 dB, u 12bitového 72 dB, zatímco 16bitový dosahuje 96 dB a 24bitový neuvěřitelných 144 dB. To je důležité, protože nyní víme, že k dokonalé reprodukci zvuku tak, jak se objevuje ve skutečném světě, potřebujeme pouze bitovou hloubku s takovým SNR, aby odpovídala dynamickému rozsahu mezi šumem na pozadí a nejhlasitějším signálem, který chceme zachytit. Je trochu složité přejít z relativních měřítek digitální oblasti na měřítka fyzického světa založená na akustickém tlaku, takže se to pokusíme zjednodušit.
Potřebujeme bitovou hloubku s dostatečným SNR, aby se přizpůsobila našemu šumu na pozadí, abychom zachytili náš zvuk tak dokonale, jak zní v reálném světě.
Vaše ucho má citlivost od 0 dB (ticho) do přibližně 120 dB (bolestivě hlasitý zvuk) a typická schopnost rozeznat hlasitost je jen 1 dB od sebe. Dynamický rozsah vašeho ucha je tedy zhruba 120 dB, tedy téměř 20 bitů.
Neslyšíte však všechno najednou, protože bubínek neboli bubínková membrána se stahuje, aby snížila množství hlasitosti, která se v hlasitém prostředí skutečně dostává do vnitřního ucha. Ani hudbu nebudete poslouchat zdaleka tak hlasitě, protože byste ohluchli. Navíc prostředí, ve kterém vy i já posloucháme hudbu, není tak tiché, jak zdravé uši slyší. Dobře ošetřené nahrávací studio nás může dostat pod 20 dB hluku na pozadí, ale poslech v rušném obývacím pokoji nebo v autobuse samozřejmě zhorší podmínky a sníží naši potřebu vysokého dynamického rozsahu.
Lidské ucho má obrovský dynamický rozsah, ale jen ne celý najednou. Maskování a ochrana sluchu snižují jeho účinnost.
K tomu všemu: s rostoucí hlasitostí se v uchu projevuje maskování vyššími frekvencemi. Při nízké hlasitosti 20 až 40 dB k maskování nedochází s výjimkou zvuků blízkých výšce. Při 80 dB se však zvuky pod 40 dB maskují, zatímco při 100 dB jsou zvuky pod 70 dB neslyšitelné. Vzhledem k dynamické povaze ucha a poslechového materiálu je obtížné uvést přesné číslo, ale skutečný dynamický rozsah vašeho sluchu je pravděpodobně v oblasti 70 dB v průměrném prostředí, až po pouhých 40 dB ve velmi hlasitém prostředí. Bitová hloubka pouhých 12 bitů by pravděpodobně pokryla většinu lidí, takže 16bitová CD nám poskytují dostatek prostoru.

hyperfyzika Při hlasitém poslechu dochází k vysokofrekvenčnímu maskování, které omezuje naše vnímání tišších zvuků.
Většina nástrojů a nahrávacích mikrofonů také vnáší šum (zejména kytarové zesilovače), a to i ve velmi tichých nahrávacích studiích. Bylo také provedeno několik studií dynamického rozsahu různých žánrů, včetně této, která ukazuje typický dynamický rozsah 60 dB. Není překvapením, že žánry s větší afinitou k tichým částem, jako je sbor, opera a klavír, vykazovaly maximální dynamický rozsah kolem 70 dB, zatímco „hlasitější“ rockové, popové a rapové žánry měly tendenci k 60 dB a méně. V konečném důsledku se hudba produkuje a nahrává pouze s takovou věrností.
Možná také znáte „války o hlasitost“ v hudebním průmyslu, které jistě popírají smysl dnešních Hi-Res audio formátů. Silné použití komprese (která zvyšuje šum a potlačuje špičky) snižuje dynamický rozsah. Moderní hudba má podstatně menší dynamický rozsah než alba před 30 lety. Teoreticky by moderní hudba mohla být distribuována s nižšími bitovými rychlostmi než stará hudba. Dynamický rozsah řady mnoha alb si můžete prohlédnout zde.

Kvalita CD je sice „jen“ 16bitová, ale pro kvalitu je to přehnané.
16 bitů je vše, co potřebujete
Toto byla docela dlouhá cesta, ale doufejme, že jste si udělali mnohem lepší představu o bitové hloubce, šumu a dynamickém rozsahu, než jsou ty zavádějící schodovité příklady, které tak často vidíte.
Bitová hloubka je především o šumu, a čím více bitů dat máte pro uložení zvuku: tím méně kvantizačního šumu se do nahrávky dostane. Ze stejného důvodu budete také schopni přesněji zachytit menší signály, což pomůže snížit úroveň digitálního šumu pod úroveň nahrávacího nebo poslechového prostředí. K tomu všemu potřebujeme bitovou hloubku. Použití obrovských bitových hloubek pro zvukové mastery nemá žádný přínos.
Překvapivě 12 bitů pravděpodobně stačí pro slušně znějící hudební master a pro uspokojení dynamického rozsahu většiny poslechových prostředí. Digitální zvuk však přenáší více než jen hudbu a příklady jako řeč nebo nahrávky prostředí pro televizi mohou využívat širší dynamický rozsah než většina hudby. Navíc trocha prostoru pro oddělení hlasitých a tichých zvuků nikdy nikomu neuškodí.
Při zachování rovnováhy 16 bitů (96 dB dynamického rozsahu nebo 120 dB s použitým ditheringem) vyhovuje široké škále typů zvuku, stejně jako limitům lidského sluchu a typickým poslechovým prostředím. Percepční nárůst 24bitové kvality je velmi diskutabilní, pokud není pouhým placebem, jak jsem doufám ukázal. Navíc nárůst velikosti souborů a šířky pásma je činí zbytečnými. Typ komprese použitý ke zmenšení velikosti souboru vaší hudební knihovny nebo streamu má mnohem znatelnější vliv na kvalitu zvuku než to, zda se jedná o 16 nebo 24bitový soubor.
.