Souhrnný úvod do logiky

9.1 Historický příklad

Filozof David Hume (1711-1776) je připomínán jako brilantní skeptický empirik. Člověk je skeptikem ohledně nějakého tématu, pokud má jednak velmi přísná měřítka pro to, co představuje poznání o daném tématu, a zároveň se domnívá, že tato přísná měřítka nemůžeme splnit. Empirismus je názor, že poznání získáváme především na základě zkušenosti, zejména smyslové. Ve své knize An Inquiry Concerning Human Understanding (Zkoumání týkající se lidského chápání) Hume stanoví své zásady pro poznání a pak nám radí, abychom si uklidili v knihovnách:

Když přebíháme po knihovnách, přesvědčeni o těchto zásadách, jakou spoušť musíme udělat? Vezmeme-li například do ruky nějaký svazek bohosloví nebo školské metafyziky, ptejme se: Obsahuje nějaké abstraktní úvahy týkající se množství nebo počtu? Ne. Obsahuje nějaké experimentální úvahy o skutečnosti a existenci? Ne. Odevzdejme ji tedy do plamenů, neboť nemůže obsahovat nic jiného než sofistiku a iluze.

Hume se domníval, že jediným zdrojem poznání je logické či matematické uvažování (které výše nazývá „abstraktní uvažování týkající se kvantity nebo čísla“) nebo smyslová zkušenost („experimentální uvažování týkající se věci skutečnosti a existence“). Huma to vede k tvrzení, že každé tvrzení, které není založeno na jedné nebo druhé metodě, je bezcenné.

Humovu argumentaci můžeme rekonstruovat následujícím způsobem. Předpokládejme, že t je nějaké téma, o němž tvrdíme, že o něm máme znalosti. Předpokládejme, že jsme toto poznání nezískali ani ze zkušenosti, ani z logiky. Anglicky napsaný jeho argument můžeme rekonstruovat následujícím způsobem:

Máme vědění o t tehdy a jen tehdy, když se naše tvrzení o t dozvíme z experimentálního uvažování nebo z logiky či matematiky.

Naše tvrzení o t se nedozvídáme z experimentálního uvažování.

Naše tvrzení o t se nedozvídáme z logiky nebo matematiky.

Nemáme znalosti o t.

Co znamená ta věta „jestliže a pouze jestliže“? Filozofové se domnívají, že se spolu s několika synonymními frázemi často používá v uvažování. Ponecháme-li „jestliže a pouze“ prozatím nevysvětlené, můžeme použít následující překladový klíč a zapsat argument ve směsi naší výrokové logiky a češtiny.

P: Máme znalosti o t.

Q: Naše tvrzení o t jsou naučená z experimentálního uvažování.

R: Naše tvrzení o t jsou naučená z logiky nebo matematiky.

A tak máme:

P jestliže a jen jestliže (QvR)

¬Q

¬R

¬P

Naším úkolem je přidat do našeho logického jazyka ekvivalent k „jestliže a jen jestliže“. Pak můžeme tuto reformulaci Humova argumentu vyhodnotit.

9.2 Dvojpodmínka

Než zavedeme symbol synonymní pro „jestliže a jen jestliže“ a pak vyložíme jeho syntax a sémantiku, měli bychom začít poznámkou. Věta typu „P jestliže a pouze jestliže Q“ se jeví jako zkrácený způsob vyjádření „P jestliže Q a P pouze jestliže Q“. Jakmile si toho všimneme, nemusíme se snažit rozeznat význam „if and only if“ pomocí našeho odborného porozumění angličtině. Místo toho můžeme rozeznat význam výrazu „if and only if“ pomocí našich již přísných definic výrazů „if“, „and“ a „only if“. Konkrétně „P if Q a P only if Q“ přeložíme „((Q→P)^(P→Q))“. (Pokud vám to není jasné, vraťte se zpět a projděte si část 2.2.) Nyní si pro tuto formuli vytvoříme pravdivostní tabulku.

.

P	Q	(Q → P)	(P → Q)	((Q→P)^(P→Q))
T	T	T	T	T	T
T	F	T	F	F
F	T	F	T	F
F	F	T	T	T

Uspořádali jsme sémantiku pro „jestliže a pouze jestliže“. Nyní můžeme zavést nový symbol pro tento výraz. Tradičně se používá dvojitá šipka „↔“. Nyní můžeme vyjádřit syntax a sémantiku „↔“:

Jsou-li Φ a Ψ věty, pak

(Φ↔Ψ)

je věta. Tento druh věty se obvykle nazývá „dvojpodmínka“.

Sémantika je dána následující pravdivostní tabulkou.

.

.

Φ	Ψ	(Φ↔Ψ)
T	T	T
T	F	F
F	T	F
F	F	T

Jedním z příjemných výsledků našeho popisu dvojpodmínky je, že nám umožňuje stručně vysvětlit syntaktický pojem logické ekvivalence. Říkáme, že dvě věty Φ a Ψ jsou „ekvivalentní“ nebo „logicky ekvivalentní“, jestliže (Φ↔Ψ) je věta.

9.3 Alternativní věty

Ukazuje se, že v angličtině existuje několik vět, které mají obvykle stejný význam jako dvojpodmínka. Každou z následujících vět bychom přeložili jako (P↔Q).

P tehdy a jen tehdy, když Q.

P právě tehdy, když Q.

P je nutné a postačující pro Q.

P je ekvivalentní Q.

9.4 Uvažování s dvojpodmínkou

Jak můžeme uvažovat pomocí dvojpodmínky? Na první pohled by se mohlo zdát, že nabízí jen málo vodítek. Vím-li, že (P↔Q), vím, že P a Q mají stejnou pravdivostní hodnotu, ale z této věty samotné nevím, zda jsou obě pravdivé, nebo obě nepravdivé. Nicméně můžeme využít sémantiky pro dvojpodmínku a pozorovat, že pokud známe i pravdivostní hodnotu jedné z vět tvořících dvojpodmínku, pak můžeme odvodit pravdivostní hodnotu druhé věty. Z toho vyplývá přímočarý soubor pravidel. Ve skutečnosti půjde o čtyři pravidla, ale my je seskupíme pod jediným názvem „ekvivalence“:

a

a

a

Co když se místo toho snažíme ukázat dvojpodmínku? Zde se můžeme vrátit k poznatku, že dvojpodmínka (Φ↔Ψ) je ekvivalentní ((Φ→Ψ)^(Ψ→Φ)). Kdybychom mohli dokázat jak (Φ→Ψ), tak (Ψ→Φ), věděli bychom, že (Φ↔Ψ) musí být pravdivé.

Toto pravidlo můžeme nazvat „dvojpodmínka“. Má následující podobu:

(Φ→Ψ)

(Ψ→Φ)

(Φ↔Ψ)

To znamená, že když chceme dokázat dvojpodmínku, často podnikneme dvě podmíněné derivace, abychom odvodili dvě podmínky, a pak použijeme pravidlo dvojpodmínky. To znamená, že mnoho důkazů dvojpodmínek má následující podobu:

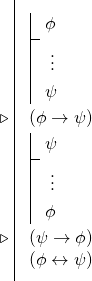
9.5 Vrátíme-li se k Humovi

Můžeme se nyní podívat, zda jsme schopni dokázat Humův argument. Vzhledem k nyní novému symbolu dvojpodmínky můžeme začít přímý důkaz s našimi třemi premisami.

Již jsme si všimli, že si myslíme, že (QvR) je nepravdivé, protože ¬Q a ¬R. Pojďme tedy dokázat ¬(QvR). Tuto větu nelze vzhledem k premisám, které máme, dokázat přímo; a nelze ji dokázat ani podmíněným důkazem, protože není podmíněná. Zkusme tedy nepřímý důkaz. Domníváme se, že ¬(QvR) je pravdivá, takže budeme předpokládat její popření a ukážeme kontradikci.

Humův argument, alespoň tak, jak jsme ho rekonstruovali, platí.

Je Humův argument správný? To, zda je zdravý, závisí na výše uvedené první premise (protože druhá a třetí premisa jsou abstrakce o nějakém tématu t). Přesněji řečeno, závisí na tvrzení, že o něčem máme vědění jen v případě, že to můžeme dokázat experimentem nebo logikou. Hume tvrdí, že bychom měli nedůvěřovat – ba dokonce bychom měli spálit texty obsahující tvrzení, která nevycházejí z experimentu a pozorování nebo z logiky a matematiky. Uvažujme však o tomto tvrzení: o nějakém tématu t máme vědění tehdy a jen tehdy, když se naše tvrzení o t dozvíme z experimentu nebo když se naše tvrzení o t dozvíme z logiky či matematiky.

Objevil Hume toto tvrzení na základě experimentů? Nebo ho objevil prostřednictvím logiky? Jaký osud by postihl Humovu knihu, kdybychom se řídili jeho radou?“

9.6 Několik příkladů

Může být užitečné dokázat některé věty, které využívají dvojpodmínky, abychom ilustrovali, jak můžeme s dvojpodmínkou uvažovat.

Tady je užitečný princip. Mají-li dvě věty stejnou pravdivostní hodnotu jako třetí věta, pak mají stejnou pravdivostní hodnotu i navzájem. Uvádíme to jako (((P↔Q)^(R↔Q))→(P↔R)). Pro ilustraci uvažování s dvojpodmínkou dokažme tuto větu.

Tato věta je podmíněná, takže bude vyžadovat podmíněné odvození. Důsledek kondicionálu je dvojpodmínka, takže budeme očekávat, že budeme potřebovat dvě podmíněná odvození, jedno k důkazu (P→R) a druhé k důkazu (R→P). Důkaz bude vypadat takto. Pozorně si ho prostudujte.

Již dříve jsme se zmínili o principech, které si spojujeme s matematikem Augustem De Morganem (1806-1871) a které se dnes nazývají „De Morganovy zákony“ nebo „De Morganovy ekvivalence“. Jedná se o poznatek, že ¬(PvQ) a (¬P^¬Q) jsou ekvivalentní, a také že ¬(P^Q) a (¬Pv¬Q) jsou ekvivalentní. Ty nyní můžeme vyjádřit pomocí dvojpodmínek. Následují věty naší logiky:

(¬(PvQ)↔(¬P^¬Q))

(¬(P^Q)↔(¬Pv¬Q))

Dokážeme druhou z těchto vět. Je to asi nejobtížnější důkaz, který jsme viděli; vyžaduje vnořené nepřímé důkazy a značnou dávku šikovnosti při hledání toho, co bude příslušnou kontradikcí.

9.7 Použití teorémů

Každá věta naší logiky je ze sémantického hlediska jedním ze tří druhů. Je to buď tautologie, věta kontradiktorická, nebo věta kontingentní. Již jsme definovali „tautologii“ (větu, která musí být pravdivá) a „kontradiktorickou větu“ (větu, která musí být nepravdivá). Kontingentní věta je věta, která není ani tautologií, ani kontradiktorickou větou. Věta kontingentní je tedy věta, která může být pravdivá, nebo může být nepravdivá.

Uveďme si příklad jednotlivých druhů vět:

(Pv¬P)

(P↔¬P)

P

První je tautologie, druhá je věta kontradiktorická a třetí je kontingentní. Můžeme se o tom přesvědčit pomocí pravdivostní tabulky.

.

P	¬P	(Pv¬P)	(P↔¬P)	P
T	F	T	F	T
F	T	T	F	F

Všimněte si, že negací tautologie je rozpor, negace kontradikce je tautologie a negace kontingentní věty je kontingentní věta.

¬(Pv¬P)

¬(P↔¬P)

¬P

.

P	¬P	(Pv¬P)	¬(Pv¬P)	(P↔¬P)	¬(P↔¬P)
T	F	T	F	F	T	T
F	T	T	F	F	T

Chvilka zamyšlení odhalí, že by bylo docela katastrofou, kdyby věta kontradiktorická nebo kontingentní byla větou naší výrokové logiky. Naše logika byla navržena tak, aby vytvářela pouze platné argumenty. Pozorovali jsme, že argumenty, které nemají žádné premisy, by měly mít závěry, které musí být pravdivé (opět to vyplývá z toho, že věta, kterou lze dokázat bez premis, by mohla být dokázána s jakýmikoli premisami, a tak by měla být raději pravdivá bez ohledu na to, jaké premisy použijeme). Pokud by věta byla kontradiktorická, věděli bychom, že můžeme dokázat nepravdu. Pokud by věta byla kontingentní, pak bychom někdy mohli dokázat nepravdu (to znamená, že bychom mohli dokázat větu, která je za určitých podmínek nepravdivá). A vzhledem k tomu, že jsme přijali nepřímé odvozování jako metodu důkazu, vyplývá z toho, že jakmile máme v argumentu kontradikci nebo kontradiktorickou větu, můžeme dokázat cokoli.

Teze nám mohou být v argumentaci velmi užitečné. Předpokládejme, že víme, že Smith ani Jones do Londýna nepojedou, a chceme tedy dokázat, že Jones do Londýna nepojede. Kdybychom si dovolili použít jeden z De Morganových teorémů, mohli bychom s argumentem rychle pracovat. Předpokládejme následující klíč:

P: Smith pojede do Londýna.

Q: Jones pojede do Londýna.

A máme následující argument:

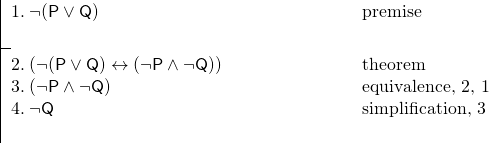
Tento důkaz jsme si velmi usnadnili použitím věty na řádku 2.

Je třeba si všimnout dvou věcí. Zaprvé bychom si to měli dovolit, protože pokud víme, že věta je věta, pak víme, že bychom tuto větu mohli dokázat v dílčím důkazu. To znamená, že bychom mohli řádek 2 výše nahradit dlouhým poddokazem, který by dokazoval (¬(P v Q)↔(¬P ^ ¬Q)), který bychom pak mohli použít. Pokud jsme si však jisti, že (¬(P v Q)↔(¬P ^ ¬Q)) je věta, neměli bychom tento důkaz provádět znovu a znovu pokaždé, když chceme větu využít.

Druhý problém, který bychom si měli uvědomit, je subtilnější. Existuje nekonečně mnoho vět ve tvaru naší věty a ty bychom měli být schopni také použít. Například následující věty by každá měla důkaz totožný s naším důkazem věty (¬(P v Q)↔(¬P ^ ¬Q)), jen písmena by byla jiná:

(¬(R v S) ↔ (¬R ^ ¬S))

(¬(T v U) ↔ (¬T ^ ¬U))

(¬(V v W) ↔ (¬V ^ ¬W))

To je snad jasné. Vezměte si důkaz (¬(P v Q)↔(¬P ^ ¬Q)) a v tomto důkazu nahraďte každý případ P za R a každý případ Q za S a dostanete důkaz (¬(R v S)↔(¬R ^ ¬S)).

Ale tady je něco, co je snad méně zřejmé. Každý z následujících důkazů si můžeme představit jako důkaz podobný důkazu (¬(P v Q)↔(¬P ^ ¬Q)).

(¬((P^Q) v (R^S))↔(¬(P^Q) ^ ¬(R^S)))

(¬(T v (Q v V))↔(¬T ^ ¬(Q v V))

(¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q)))

Např, kdybychom vzali důkaz (¬(P v Q)↔(¬P ^ ¬Q)) a každý počáteční případ P nahradili (Q↔P) a každý počáteční případ Q nahradili (¬R→¬Q), pak bychom měli důkaz věty (¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q))).

Tento poznatek bychom mohli zachytit dvěma způsoby. Mohli bychom uvést věty našeho metajazyka a připustit, že mají instance. Tak bychom mohli vzít (¬(Φ v Ψ) ↔ (¬Φ ^ ¬Ψ)) jako větu metajazyka, v němž bychom mohli každé Φ nahradit větou a každé Ψ větou a získat konkrétní instanci věty. Alternativou je připustit, že z věty můžeme substitucí vytvořit další věty. Pro usnadnění zvolíme tuto druhou strategii.

Naše pravidlo bude následující. Jakmile jednou dokážeme větu, můžeme ji kdykoli citovat v důkazu. Naše zdůvodnění spočívá v tom, že tvrzení je věta. Povolíme záměnu libovolné atomické věty v tvrzení za libovolnou jinou větu tehdy a jen tehdy, když každý počáteční případ této atomické věty v tvrzení nahradíme stejnou větou.

Než se budeme zabývat příkladem, je výhodné uvést několik užitečných tezí. Teoremat našeho jazyka je nekonečně mnoho, ale těchto deset je často velmi užitečných. Několik z nich jsme již dokázali. Ostatní lze dokázat jako cvičení.

T1 (P v ¬P)

T2 (¬(P→Q) ↔ (P^¬Q))

T3 (¬(P v Q) ↔ (¬P ^ ¬Q))

T4 ((¬P v ¬Q) ↔ ¬(P ^ Q))

T5 (¬(P ↔ Q) ↔ (P ↔ ¬Q))

T6 (¬P → (P → Q))

T7 (P → (Q → P))

T8 ((P→(Q→R)) → ((P→Q) → (P→R)))

T9 ((¬P→¬Q) → ((¬P→Q) →P))

T10 ((P→Q) → (¬Q→¬P))

Několik příkladů nám objasní výhodu používání teorémů. Uvažujme jiný argument, který vychází z výše uvedeného. Víme, že neplatí ani to, že když Smith pojede do Londýna, pojede do Berlína, ani to, že když Jones pojede do Londýna, pojede do Berlína. Chceme dokázat, že není případ, že Jones pojede do Berlína. Do našeho klíče doplníme následující:

R: Smith pojede do Berlína.

S: Smith pojede do Berlína: Jones pojede do Berlína.

A máme následující argument:

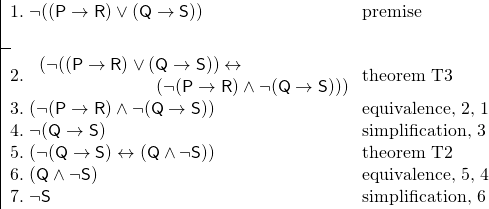
Při použití teorémů byl tento důkaz mnohem kratší, než by jinak mohl být. Teorémy také často usnadňují sledování důkazu, protože je rozpoznáváme jako tautologie – jako věty, které musí být pravdivé.

9.8 Úlohy

1. Dokažte, že každý z následujících argumentů platí.

1. Předpoklady: P, ¬Q. Závěr: ¬(P↔Q).
2. Předpoklady: (¬PvQ), (Pv¬Q). Závěr: PvQ, PvQ, PvQ, PvQ, PvQ: (P↔Q).
3. Předpoklady: (P↔Q), (R↔S) . Závěr: ((P^R)↔(Q^S)).

1. Dokažte každou z následujících vět.

1. T1
2. T2
3. T5
4. T6
5. T7
6. T8
7. T9
8. ((P^Q)↔¬(¬Pv¬Q)).
9. ((P→Q)↔¬(P^¬Q))

1. V běžné hovorové češtině napište vlastní platný argument s alespoň dvěma premisami, z nichž alespoň jedna je dvojpodmínka. Váš argument by měl mít podobu pouhého odstavce (nikoli uspořádaného seznamu vět nebo čehokoli jiného, co by se podobalo formální logice). Přeložte jej do výrokové logiky a dokažte, že je platný.
2. V běžné hovorové angličtině napište vlastní platný argument s alespoň dvěma premisami a se závěrem, který je dvojpodmínkou. Váš argument by měl mít podobu pouhého odstavce (nikoli uspořádaného seznamu vět nebo čehokoli jiného, co vypadá formálně jako logika). Přeložte jej do výrokové logiky a dokažte, že je platný.