Družice je těleso, které se pohybuje kolem jiného tělesa po matematicky předvídatelné dráze zvané dráha. Komunikační družice není nic jiného než mikrovlnná opakovací stanice ve vesmíru, která je užitečná v telekomunikacích, rozhlase a televizi spolu s internetovými aplikacemi.
Opakovač je obvod, který zvyšuje sílu přijímaného signálu a znovu jej vysílá. Zde však tento opakovač funguje jako transpondér, který mění frekvenční pásmo vysílaného signálu oproti přijímanému.
Frekvence, se kterou je signál vysílán do vesmíru, se nazývá frekvence Uplink, zatímco frekvence, se kterou je vysílán transpondérem, je frekvence Downlink.
Následující obrázek tento koncept jasně ilustruje.
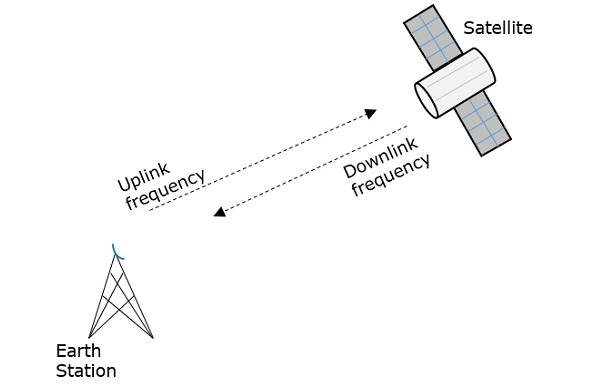
Nyní se podívejme na výhody, nevýhody a aplikace satelitní komunikace.
Satelitní komunikace – výhody
Existuje mnoho výhod satelitní komunikace, jako například –
-
Flexibilita
-
Snadná instalace nových okruhů
-
Snadno se překonávají vzdálenosti a nezáleží na nákladech
-
Vysílání. možnosti
-
Každý kout Země je pokryt
-
Uživatel může síť ovládat
Satelitní komunikace – nevýhody
Satelitní komunikace má následující nevýhody –
-
Počáteční náklady, jako jsou náklady na segment a start, jsou příliš vysoké.
-
Zatížení frekvencí
-
Rušení a šíření
Satelitní komunikace – aplikace
Satelitní komunikace nachází uplatnění v následujících oblastech –
-
V rozhlasovém vysílání.
-
V televizním vysílání, jako je DTH.
-
V internetových aplikacích, jako je poskytování internetového připojení pro přenos dat, aplikace GPS, surfování po internetu atd.
-
Pro hlasovou komunikaci.
-
Pro sektor výzkumu a vývoje, v mnoha oblastech.
-
Ve vojenských aplikacích a navigaci.
Orientace družice na její dráze závisí na třech zákonech, které se nazývají Keplerovy zákony.
Keplerovy zákony
Johannes Kepler (1571-1630), astronomický vědec, podal 3 revoluční zákony, týkající se pohybu družic. Dráha, po které družice obíhá kolem svého primáru (Země), je elipsa. Elipsa má dvě ohniska – F1 a F2, přičemž jedním z nich je Země.
Uvažujeme-li vzdálenost středu objektu od bodu na jeho eliptické dráze, pak nejvzdálenější bod elipsy od středu se nazývá apogeum a nejkratší bod elipsy od středu se nazývá perigeum.
Keplerův 1. zákon
Keplerův 1. zákon říká, že „každá planeta obíhá kolem Slunce po eliptické dráze, přičemž Slunce je jedním z jejích ohnisek“. Družice jako taková se pohybuje po eliptické dráze, jejímž jedním z ohnisek je Země.
Polohová hlavní osa elipsy se označuje jako „a“ a polohová vedlejší osa jako „b“. Proto lze excentricitu e této soustavy zapsat jako –
$$e = \frac{\sqrt{a^{2}-b^{2}}}{a}$$
-
Eccentricita (e) – Je to parametr, který určuje rozdíl ve tvaru elipsy a ne kružnice.
-
Semi-větší osa (a) – Je to nejdelší průměr vedený spojnicí dvou ohnisek podél středu, který se dotýká obou apogeí (nejvzdálenějších bodů elipsy od středu).
-
Poloměrná osa (b) – Je to nejkratší průměr vedený středem, který se dotýká obou perigeí (nejkratších bodů elipsy od středu).
Ty jsou dobře popsány na následujícím obrázku.
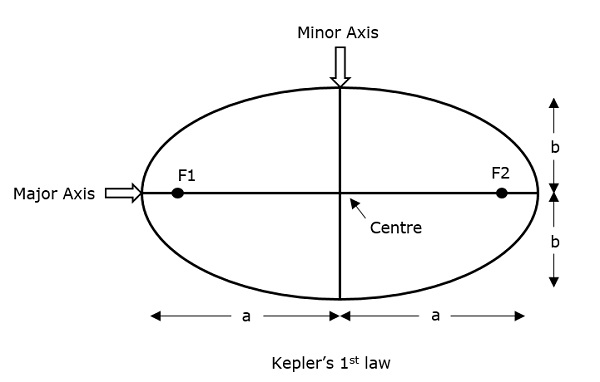
Pro eliptickou dráhu je vždy žádoucí, aby excentricita ležela v rozmezí 0 až 1, tzn.tj. 0 < e < 1, protože pokud e nabývá nulové hodnoty, dráha již nebude mít eliptický tvar, spíše se změní na dráhu kruhovou.
Druhý Keplerův zákon
Druhý Keplerův zákon říká: „Pro stejné časové intervaly je plocha, kterou družice pokryje, vzhledem ke středu Země stejná.“
To lze pochopit, když se podíváme na následující obrázek.
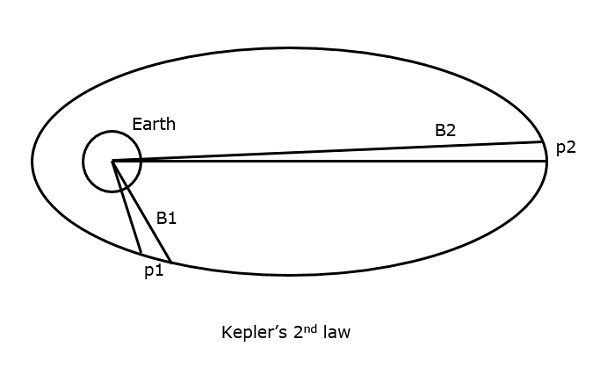
Předpokládejme, že družice urazí za stejný časový interval vzdálenosti p1 a p2, pak plochy B1 a B2, které urazí v obou případech, jsou stejné.
Třetí Keplerův zákon
Třetí Keplerův zákon říká: „Čtverec periodické doby oběhu je úměrný krychli střední vzdálenosti obou těles.“
Tento zákon lze matematicky zapsat jako
$$T^{2}\:\alfa\:\:a^{3}$$
což znamená
$$T^{2} = \frac{4\pi ^{2}}{GM}a^{3}$$
kde $\frac{4\pi ^{2}}{GM}$ je konstanta úměrnosti. (podle Newtonovy mechaniky)
$$T^{2} = \frac{4\pi ^{2}}{\mu}a^{3}$$
Kde μ = geocentrická gravitační konstanta Země, i.Μ = 3.986005 × 1014 m3/sec2
$$1 = \left ( \frac{2\pi}{T} \right )^{2}\frac{a^{3}}{\mu}$$
$$1 = n^{2}\frac{a^{3}}{\mu}\:\:\:\Rightarrow \:\:a^{3} = \frac{\mu}{n^{2}}$$
Kde n = střední pohyb družice v radiánech za sekundu
Pomocí těchto Keplerových zákonů se počítá orbitální fungování družic.
Současně s nimi je třeba upozornit na jednu důležitou věc. Družice při oběhu kolem Země podléhá přitažlivé síle Země, což je gravitační síla. Také na ni působí určitá přitažlivá síla od Slunce a Měsíce. Působí na ni tedy dvě síly. Jsou to –
-
Síla dostředivá – Síla, která má tendenci přitahovat objekt pohybující se po dráze k sobě, se nazývá dostředivá síla.
-
Síla odstředivá – Síla, která má tendenci vytlačovat objekt pohybující se po dráze od své polohy, se nazývá odstředivá síla.
Satelit tedy musí tyto dvě síly vyrovnávat, aby se udržel na své oběžné dráze.
Oběžné dráhy
Satelit při vypuštění do vesmíru musí být umístěn na určité oběžné dráze, která zajistí určitý způsob jeho otáčení, aby byla zachována jeho dostupnost a mohl sloužit svému účelu, ať už vědeckému, vojenskému nebo komerčnímu. Takové oběžné dráhy, které jsou družicím přiděleny, se vzhledem k Zemi nazývají oběžné dráhy Země. Družice na těchto oběžných drahách se nazývají družice na oběžné dráze Země.
Důležité druhy oběžných drah Země jsou –
-
Geosynchronní oběžná dráha Země
-
Střední oběžná dráha Země
-
Nízká oběžná dráha Země
Geosynchronní oběžná dráha Země Satelity
GeoSynchronní oběžná dráha Země (GEO) je družice, která je umístěna ve výšce 22,300 mil nad Zemí. Tato oběžná dráha je synchronizována se stranou skutečného dne (tj. 23 hodin 56 minut). Tato dráha může mít sklon a excentricitu. Nemusí být kruhová. Tato oběžná dráha může být nakloněna na zemských pólech. Při pozorování ze Země se však jeví jako stacionární.
Táž geosynchronní dráha, je-li kruhová a v rovině rovníku, se nazývá geostacionární dráha. Tyto družice jsou umístěny ve výšce 35 900 km (stejně jako geosynchronní) nad zemským rovníkem a stále se otáčejí vzhledem k zemskému směru (ze západu na východ). Tyto družice jsou považovány za stacionární vzhledem k Zemi, z čehož vyplývá i jejich název.
Satelity na geostacionární dráze Země se používají pro předpověď počasí, satelitní televizi, satelitní rádio a další typy globální komunikace.
Následující obrázek ukazuje rozdíl mezi geosynchronní a geostacionární dráhou. Osa otáčení označuje pohyb Země.
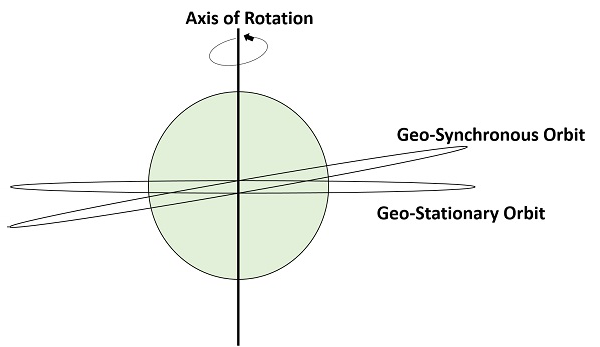
Poznámka – Každá geostacionární dráha je geosynchronní dráha. Ale každá geosynchronní dráha NENÍ geostacionární dráha.
Satelity na střední oběžné dráze Země
Sítě satelitů na střední oběžné dráze Země (MEO) budou obíhat ve vzdálenosti asi 8000 mil od zemského povrchu. Signály vysílané ze satelitu MEO urazí kratší vzdálenost. To znamená lepší sílu signálu na přijímací straně. Z toho vyplývá, že na přijímací straně lze použít menší a lehčí přijímací terminály.
Protože signál cestuje na kratší vzdálenost k družici a z družice, je menší zpoždění přenosu. Přenosové zpoždění lze definovat jako dobu, kterou potřebuje signál k cestě na satelit a zpět k přijímací stanici.
Pro komunikaci v reálném čase platí, že čím kratší je přenosové zpoždění, tím lepší bude komunikační systém. Jako příklad lze uvést, že pokud družice GEO potřebuje na cestu tam a zpět 0,25 sekundy, pak družice MEO potřebuje k dokončení stejné cesty méně než 0,1 sekundy. Družice MEO pracují ve frekvenčním rozsahu 2 GHz a vyšším.
Satelity na nízké oběžné dráze Země
Satelity na nízké oběžné dráze Země (LEO) se dělí především do tří kategorií, a to na malé LEO, velké LEO a Mega LEO. Družice LEO obíhají ve vzdálenosti 500 až 1000 mil nad zemským povrchem.
Tato relativně krátká vzdálenost snižuje zpoždění přenosu na pouhých 0,05 sekundy. To dále snižuje potřebu citlivých a objemných přijímacích zařízení. Malé LEO budou pracovat v pásmu 800 MHz (0,8 GHz). Velké LEO budou pracovat v pásmu 2 GHz nebo vyšším a Mega-LEO pracují v pásmu 20-30 GHz.
Vyšší frekvence spojené s Mega-LEO se promítají do větší kapacity přenosu informací a přinášejí možnost schématu přenosu videa v reálném čase s malým zpožděním.
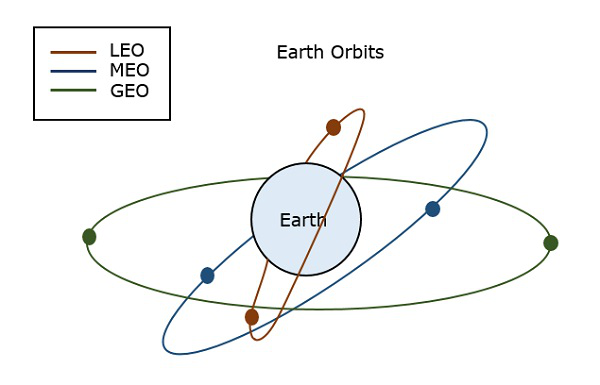
Následující obrázek znázorňuje dráhy LEO, MEO a GEO.
.