Směrodatná odchylka je průměrné množství variability v souboru dat. Říká vám v průměru, jak daleko leží každá hodnota od průměru.
Vysoká směrodatná odchylka znamená, že hodnoty jsou obecně daleko od průměru, zatímco nízká směrodatná odchylka naznačuje, že hodnoty jsou seskupeny blízko průměru.
Co vám říká směrodatná odchylka?
Směrodatná odchylka je užitečným měřítkem rozptylu pro normální rozdělení.
V normálním rozdělení jsou data symetricky rozložena bez zkreslení. Většina hodnot se shlukuje kolem centrální oblasti, přičemž se vzdáleností od středu se hodnoty zužují. Směrodatná odchylka udává, jak jsou data v průměru rozprostřena od středu rozdělení.
Mnoho vědeckých proměnných se řídí normálním rozdělením, včetně výšky, standardizovaných výsledků testů nebo hodnocení spokojenosti s prací. Když máte k dispozici směrodatné odchylky různých vzorků, můžete pomocí statistických testů porovnat jejich rozdělení a vyvodit závěry o větších populacích, ze kterých pocházejí.
Průměrná hodnocení (M) jsou pro každou skupinu stejná – je to hodnota na ose x, kdy je křivka na svém vrcholu. Jejich směrodatné odchylky (SD) se však navzájem liší.
Směrodatná odchylka odráží rozptyl rozdělení. Křivka s nejnižší směrodatnou odchylkou má vysoký vrchol a malý rozptyl, zatímco křivka s nejvyšší směrodatnou odchylkou je plošší a rozsáhlejší.
Empirické pravidlo
Směrodatná odchylka a střední hodnota vám společně mohou říci, kde leží většina hodnot ve vašem rozdělení, pokud se řídí normálním rozdělením.
Empirické pravidlo neboli pravidlo 68-95-99,7 vám řekne, kde leží hodnoty vašeho rozdělení:
- Přibližně 68 % výsledků se nachází do 2 směrodatných odchylek od průměru,
- Přibližně 95 % výsledků se nachází do 4 směrodatných odchylek od průměru,
- Přibližně 99 % výsledků se nachází do 4 směrodatných odchylek od průměru.7 % skóre je v rozmezí 6 směrodatných odchylek od průměru.
Podle empirického pravidla:
- Přibližně 68 % výsledků je v rozmezí 40 až 60.
- Přibližně 95 % výsledků je v rozmezí 30 až 70.
- Podle empirického pravidla:
- Přibližně 68 % výsledků je v rozmezí 30 až 70.
- Přibližně 99,7 % skóre je mezi 20 a 80.
Empirické pravidlo je rychlý způsob, jak získat přehled o datech a zkontrolovat případné odlehlé nebo extrémní hodnoty, které se neřídí tímto vzorem.
U nenormálních rozdělení je směrodatná odchylka méně spolehlivým měřítkem variability a měla by se používat v kombinaci s dalšími měřítky, jako je rozsah nebo mezikvartilové rozpětí.
Vzorce pro výpočet směrodatné odchylky pro populace a vzorky
Pro výpočet směrodatných odchylek se používají různé vzorce podle toho, zda máte data z celé populace nebo ze vzorku.
Standardní odchylka populace
Pokud jste shromáždili údaje od všech členů populace, která vás zajímá, můžete získat přesnou hodnotu standardní odchylky populace.
Vzorce pro populační směrodatnou odchylku vypadá následovně:
| vzorec | Vysvětlení |
|---|---|
 |
|
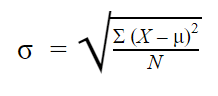Výběrová směrodatná odchylka
Při sběru dat ze vzorku se výběrová směrodatná odchylka používá k odhadům nebo závěrům o populační směrodatné odchylce.
Výběrová směrodatná odchylka vypadá takto:
| vzorec | Vysvětlení |
|---|---|
 |
|
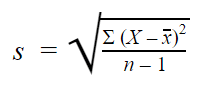U vzorků používáme ve vzorci n – 1, protože použitím n bychom získali zkreslený odhad, který by trvale podhodnocoval variabilitu. Směrodatná odchylka vzorku by měla tendenci být nižší než skutečná směrodatná odchylka populace.
Snížením výběrového n na n – 1 se směrodatná odchylka uměle zvětší, čímž získáme konzervativní odhad variability.
Ačkoli se nejedná o nestranný odhad, je to méně zkreslený odhad směrodatné odchylky: je lepší variabilitu ve vzorcích nadhodnocovat než podhodnocovat.
Kroky pro výpočet směrodatné odchylky
Směrodatnou odchylku obvykle automaticky vypočítá ten který software, který používáte pro statistickou analýzu. Můžete ji však také vypočítat ručně, abyste lépe pochopili, jak vzorec funguje.
Při ručním zjišťování směrodatné odchylky existuje šest hlavních kroků. K projití jednotlivých kroků použijeme malý soubor dat o 6 skórech.
| Soubor dat | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
1. krok: Zjištění průměru
Pro zjištění průměru sečtěte všechna skóre a poté je vydělte počtem skóre.
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50
Krok 2: Zjistěte odchylku každého skóre od průměru
Od každého skóre odečtěte průměr, abyste získali odchylky od průměru.
Protože x̅ = 50, zde odečteme 50 od každého skóre.
| Skóre | Odchylka od průměru |
|---|---|
| 46 | 46 – 50 = -.4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
Krok 3: Každou odchylku od průměru odmocněte
Každou odchylku od průměru vynásobte sebou samým. Výsledkem budou kladná čísla.
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -.18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81
Krok 4: Najděte součet čtverců
Sečtěte všechny čtvercové odchylky. Tomu se říká součet čtverců.
16 + 361 + 324 + 100 + 4 + 81 = 886
Krok 5: Najděte rozptyl
Součet čtverců vydělte n – 1 (u vzorku) nebo N (u populace) – to je rozptyl.
Protože pracujeme se vzorkem o velikosti 6, použijeme n – 1, kde n = 6.
886 ÷ (6 – 1) = 886 ÷ 5 = 177. Varianty jsou tedy následující.2
Krok 6: Nalezení druhé odmocniny z rozptylu
Pro nalezení směrodatné odchylky vezmeme druhou odmocninu z rozptylu.
√177,2 = 13,31
Z učení, že SD = 13.31, můžeme říci, že každý výsledek se v průměru odchyluje od průměru o 13,31 bodu.
Proč je směrodatná odchylka užitečným měřítkem variability?
Přestože existují jednodušší způsoby výpočtu variability, vzorec pro výpočet směrodatné odchylky váží nerovnoměrně rozložené vzorky více než rovnoměrně rozložené vzorky. Vyšší směrodatná odchylka vám říká, že rozdělení je nejen více rozptýlené, ale také více nerovnoměrně rozložené.
To znamená, že vám dává lepší představu o variabilitě dat než jednodušší míry, jako je střední absolutní odchylka (MAD).
MAD je podobná směrodatné odchylce, ale snadněji se počítá. Nejprve vyjádříte každou odchylku od průměru v absolutních hodnotách tak, že je převedete na kladná čísla (například z -3 se stane 3). Poté vypočtete průměr těchto absolutních odchylek.
Na rozdíl od směrodatné odchylky nemusíte u MAD počítat čtverce nebo odmocniny z čísel. Z tohoto důvodu však poskytuje méně přesnou míru variability.
Vezměme dva vzorky se stejnou centrální tendencí, ale různou velikostí variability. Vzorek B je variabilnější než vzorek A.
| Hodnoty | Střední hodnota | Střední absolutní odchylka | Standardní odchylka | |
|---|---|---|---|---|
| Vzorek A | 66. Jaký je průměr? 30, 40, 64 | 50 | 15 | 17.8 |
| Vzor B | 51, 21, 79, 49 | 50 | 15 | 23,7 |
U vzorků se stejnými průměrnými odchylkami od průměru nelze pomocí MAD rozlišit úrovně rozpětí. Směrodatná odchylka je přesnější: je vyšší u vzorku s větší variabilitou odchylek od průměru.
Díky kvadratizaci odchylek od průměru odráží směrodatná odchylka nerovnoměrný rozptyl přesněji. Tento krok váží extrémní odchylky více než malé odchylky.
Tím se však směrodatná odchylka stává citlivější na odlehlé hodnoty.
Často kladené otázky o směrodatné odchylce
Variabilita se nejčastěji měří pomocí následujících popisných statistik:
- Rozsah: rozdíl mezi nejvyšší a nejnižší hodnotou
- Mezikvartilový rozsah: Rozsah střední poloviny rozdělení
- Směrodatná odchylka: průměrná vzdálenost od průměru
- Rozptyl: průměr čtverců vzdáleností od průměru
Standardní odchylka je průměrná velikost variability ve vašem souboru dat. Říká vám v průměru, jak daleko leží jednotlivé výsledky od průměru.
V normálním rozdělení vysoká směrodatná odchylka znamená, že hodnoty jsou obecně daleko od průměru, zatímco nízká směrodatná odchylka naznačuje, že hodnoty jsou seskupeny blízko průměru.
V normálním rozdělení jsou data rozložena symetricky bez zkreslení. Většina hodnot se shlukuje kolem centrální oblasti, přičemž se vzdáleností od středu se hodnoty zužují.
Míry centrální tendence (průměr, modus a medián) jsou v normálním rozdělení přesně stejné.
Empirické pravidlo neboli pravidlo 68-95-99,7 říká, kde leží většina hodnot v normálním rozdělení:
- Přibližně 68 % hodnot se nachází uvnitř 1 směrodatné odchylky od průměru.
- Přibližně 95 % hodnot se nachází uvnitř 2 směrodatných odchylek od průměru.
- Přibližně 99 % hodnot se nachází uvnitř 1 směrodatné odchylky od průměru.
- Přibližně 100 % hodnot se nachází uvnitř 2 směrodatných odchylek od průměru.
- Přibližně 100 % hodnot se nachází uvnitř 2 směrodatných odchylek od průměru.7 % hodnot je v rozmezí 3 směrodatných odchylek od průměru.
Empirické pravidlo je rychlý způsob, jak získat přehled o datech a zkontrolovat případné odlehlé nebo extrémní hodnoty, které se neřídí tímto vzorem.
Variance je průměrná kvadratická odchylka od průměru, zatímco směrodatná odchylka je odmocnina z tohoto čísla. Obě míry odrážejí variabilitu rozdělení, ale jejich jednotky se liší:
- Standardní odchylka se vyjadřuje ve stejných jednotkách jako původní hodnoty (např. minuty nebo metry).
- Variabilita se vyjadřuje v mnohem větších jednotkách (např. metry na druhou).
Ačkoli jednotky variability je obtížnější intuitivně pochopit, variabilita je důležitá ve statistických testech.
Variabilita je důležitá ve statistických testech.