Odpověď 7 – 7 – 7 = 73 To se čte „sedm na kostku“

Porozumění exponentům a odmocninám

Cíl(e) výuky

– Vyhodnotit výrazy obsahující exponenty.

– Zapsat opakované činitele pomocí exponenciálního zápisu.

– Najít odmocninu z dokonalého čtverce.

Exponenty poskytují zvláštní způsob zápisu opakovaného násobení. Čísla zapsaná tímto způsobem mají specifický tvar, přičemž každá část poskytuje důležitou informaci o čísle. Zápis čísel pomocí exponentů může také ušetřit mnoho místa. Inverzní operace násobení čísla sebou samým se nazývá nalezení odmocniny z čísla. Tato operace je užitečná při řešení úloh o ploše čtverce.

Exponenciální zápis je speciální způsob zápisu opakovaných činitelů, například 7 – 7. V případě, že se jedná o opakovaný činitel, je možné jej zapsat do zápisu. Exponenciální zápis má dvě části. Jedna část zápisu se nazývá základ. Základem je číslo, které se násobí samo sebou. Druhou částí zápisu je exponent neboli mocnina. To je malé číslo zapsané vysoko vpravo od základu. Exponent neboli mocnina říká, kolikrát se má základ použít jako činitel při násobení. V příkladu 7 – 7 lze zapsat jako 72, 7 je základ a 2 je exponent. Exponent 2 znamená, že se jedná o dva činitele.

72 = 7 – 7 = 49

Číslo 72 můžete číst jako „sedm na druhou“. Je to proto, že násobení čísla sebou samým se nazývá „odmocňování čísla“. Podobně zvyšování čísla na mocninu 3 se nazývá „kubizace čísla“. Číslo 73 můžete číst jako „sedm v kostce“.

Číslo 25 můžete číst jako „dvě na pátou mocninu“ nebo „dvě na mocninu pěti“. Číslo 84 můžete číst jako „osm na čtvrtou mocninu“ nebo „osm na mocninu čtyř“. Tento formát lze použít pro čtení jakéhokoli čísla zapsaného v exponenciálním zápisu. Ve skutečnosti se číslo 63 sice nejčastěji čte jako „šest na kubík“, ale lze ho také číst jako „šest na třetí mocninu“ nebo „šest na mocninu tří“.

Chcete-li zjistit hodnotu čísla zapsaného v exponenciálním tvaru, přepište číslo jako opakované násobení a proveďte násobení. Níže jsou uvedeny dva příklady.

Zjistěte hodnotu čísla 43. Jaká je hodnota čísla 43?

A) 12

B) 64

C) 256

D) 43

Zápis opakovaného násobení v exponenciálním zápisu může ušetřit čas i místo. Vezměme si příklad 5 – 5 – 5 – 5. Toto opakované násobení můžeme pomocí exponenciálního zápisu zapsat jako 54. Protože se násobí číslem 5, zapíšeme ho jako základ. Protože základ je při násobení použit čtyřikrát, exponent je 4. Výraz 5 – 5 – 5 – 5 lze přepsat ve zkráceném exponenciálním zápisu jako 54 a čte se: „pět na čtvrtou mocninu“ nebo „pět na mocninu 4.“

Chceme-li opakované násobení téhož čísla zapsat v exponenciálním zápisu, napíšeme nejprve násobené číslo jako základ. Poté spočítejte, kolikrát je toto číslo při násobení použito, a toto číslo zapište jako exponent. Při určování exponentu nezapomeňte počítat čísla, nikoli znaménka násobení.

Zapište 10 – 10 – 10 – 10 – 10 – 10 v exponenciálním zápisu.

A) 1 000 000

B) 60

C) 105

D) 106

Jak jste viděli dříve, číslu 52 se říká „pět na druhou“. „Pět na druhou“ znamená násobení pěti sebou samým. V matematice nazýváme násobení čísla sebou samým „odmocňováním“ čísla. Výsledek odmocnění celého čísla nazýváme čtverec nebo dokonalý čtverec. Dokonalý čtverec je každé číslo, které lze zapsat jako celé číslo zvýšené na mocninu 2. Například 9 je dokonalý čtverec. Dokonalé čtvercové číslo lze znázornit jako čtverec, jak je znázorněno níže. Vidíme, že 1, 4, 9, 16, 25 a 36 jsou příklady dokonalých čtverců.

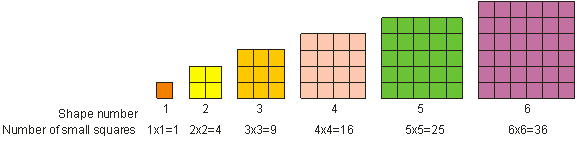
Chceme-li číslo odmocnit, vynásobíme je sami sebou. Čtverec 3 = 32 = 3 – 3 = 9.

Níže jsou uvedeny další příklady dokonalých čtverců.

Opětná operace odmocňování čísla se nazývá nalezení odmocniny z čísla. Nalezení odmocniny je jako otázka „jaké číslo vynásobené sebou samým mi dá toto číslo?“. Druhá odmocnina čísla 25 je 5, protože 5 vynásobené sebou samým se rovná 25. Druhé odmocniny se zapisují pomocí matematického symbolu, kterému se říká znaménko radikálu a který vypadá takto: . „Druhá odmocnina z 25“ se píše .

Najít .

A) 6

B) 18

C) 72

D) 7

Exponenciální zápis je zkrácený způsob zápisu opakovaného násobení stejného čísla. Číslo zapsané v exponenciálním zápisu má základ a exponent a každá z těchto částí poskytuje informace pro zjištění hodnoty výrazu. Základ říká, jaké číslo je opakovaně násobeno, a exponent říká, kolikrát je základ při násobení použit. Exponenty 2 a 3 mají speciální názvy. Zvyšování základu na mocninu 2 se nazývá „odmocňování“ čísla. Zvyšování základu na mocninu 3 se nazývá „kubizace“ čísla. Opakem odmocňování čísla je hledání odmocniny z čísla. Chcete-li najít druhou odmocninu čísla, položte si otázku: „Jaké číslo mohu vynásobit sebou samým, abych dostal toto číslo?“

.