
The Policy Question: Daňová úleva na nákup hybridních automobilů – je to nejlepší volba vlády pro snížení spotřeby paliva a emisí uhlíku?
Obyvatelé USA a vláda jsou znepokojeni závislostí na dovozu zahraniční ropy a vypouštěním uhlíku do atmosféry. V roce 2005 přijal Kongres zákon, který spotřebitelům poskytuje daňové úlevy na nákup elektrických a hybridních automobilů.
Tato daňová úleva se může zdát jako dobrá politická volba, ale je nákladná, protože přímo snižuje objem příjmů, které americká vláda vybere. Existují účinnější přístupy ke snížení závislosti na fosilních palivech a emisí uhlíku? Jak se rozhodneme, která politika je nejlepší? K zodpovězení této otázky potřebují tvůrci politiky s určitou přesností předpovědět, jak budou spotřebitelé na tuto daňovou politiku reagovat, dříve než tito tvůrci politiky vynaloží miliony federálních dolarů.
Na tuto politickou otázku můžeme použít koncept užitečnosti. V tomto modulu se budeme zabývat užitkem a funkcemi užitku. Budeme pak schopni použít vhodnou funkci užitku k odvození indiferenčních křivek, které popisují naši politickou otázku.
Zkoumání politické otázky
Předpokládejme, že daňová úleva na dotování nákupu hybridních automobilů je mimořádně úspěšná a zdvojnásobí průměrnou spotřebu paliva všech automobilů na amerických silnicích – výsledek, který zjevně není reálný, ale je užitečný pro naše další diskuse. Co myslíte, že by se stalo se spotřebou paliva všech amerických motoristů? Měla by vláda v reakci na to očekávat snížení spotřeby paliva a emisí uhlíku z automobilů na polovinu? Proč, nebo proč ne?“
2.1 Funkce užitku
LO 2.1: Jaké jsou funkce užitku?
2.2 Funkce užitku a typické preference
LO 2.2: Popište funkci užitku: Identifikovat funkce užitku na základě typických preferencí, které reprezentují.
2.3 Vztah mezi funkcemi užitku a mapami indiferenčních křivek
LO 2.3: Vysvětlit, jak z funkce užitku odvodit indiferenční křivku.
2.4 Zjištění mezního užitku a mezní míry substituce
LO 2.4: Odvodit mezní užitek a MRS pro typické funkce užitku.
2.5: Odvodit mezní užitek a MRS pro typické funkce užitku. Politická otázka
2.1 Funkce užitku
LO1: Popište funkci užitku.
Naše preference nám umožňují porovnávat různé spotřební balíčky a vybírat preferované balíčky. Na základě našich preferencí můžeme například určit pořadí celého souboru svazků. Funkce užitku je matematická funkce, která řadí balíčky spotřebních statků tak, že každému přiřadí číslo, kde větší čísla označují preferované balíčky. Funkce užitku mají vlastnosti, které jsme identifikovali v modulu 1, pokud jde o preference. To znamená: jsou schopny uspořádat balíčky, jsou úplné a tranzitivní, více je preferováno před méně a v relevantních případech jsou lepší smíšené balíčky.
Číslo, které funkce užitku přiřadí určitému balíčku, se nazývá užitek, uspokojení, které spotřebitel získává z určitého balíčku. Číslo užitku pro každý svazek neznamená nic v absolutním vyjádření; neexistuje žádné jednotné měřítko, podle kterého bychom spokojenost měřili. Má pouze relativní význam: pomocí užitku můžeme určit, které svazky jsou preferovány před jinými.
Je-li užitek ze svazku A vyšší než užitek ze svazku B, je to ekvivalentní tvrzení, že spotřebitel preferuje svazek A před svazkem B. Funkce užitku tedy řadí preference spotřebitelů tak, že každému svazku přiřadí určité číslo. . Funkci užitku můžeme použít k vykreslení map indiferenční křivky popsaných v modulu 1. Protože všechny balíčky na stejné indiferenční křivce poskytují stejné uspokojení, a žádný z nich tedy není preferován, má každý balíček stejný užitek. Můžeme tedy nakreslit indiferenční křivku tak, že určíme všechny svazky, které z funkce užitku vracejí stejné číslo.
Ekonomové říkají, že funkce užitku jsou spíše ordinální než kardinální. Ordinální znamená, že funkce užitku pouze řadí svazky – udává pouze, který z nich je lepší, nikoliv o kolik je lepší než jiný svazek. Předpokládejme například, že jedna funkce užitku udává, že svazek A přináší 10 užitků a svazek B 20 užitků. Neříkáme, že svazek B je dvakrát tak dobrý nebo o 10 užitků lepší, pouze že spotřebitel dává přednost svazku B. Předpokládejme například, že se kamarádka zúčastnila závodu a řekla vám, že skončila třetí. Tato informace je ordinální: Víte, že byla rychlejší než závodník na čtvrtém místě a pomalejší než závodník na druhém místě. Znáte pouze pořadí, v jakém běžci doběhli. Jednotlivé časy jsou kardinální: Protože funkce užitku jsou ordinální, mnoho různých funkcí užitku může reprezentovat stejné preference. To platí, pokud je zachováno pořadí.
Příklad funkce užitku U, která popisuje preference nad svazky zboží A abd B: U(A,B). Na tuto funkci můžeme aplikovat libovolnou kladnou monotónní transformaci (což v podstatě znamená, že neměníme uspořádání) a nová funkce, kterou jsme vytvořili, bude reprezentovat stejné preference. Můžeme například vynásobit kladnou konstantu α nebo přičíst kladnou či zápornou konstantu β . Takže αU(A,B)+β reprezentuje přesně stejné preference jako U(A,B), protože bude uspořádávat svazky přesně stejným způsobem. Tato skutečnost je docela užitečná, protože někdy použití kladné monotónní transformace funkce užitku usnadňuje řešení problémů.
2.2 Funkce užitku a typické preference
LO2: Určete funkce užitku na základě typických preferencí, které reprezentují
Považujte svazky jablek A a banánů B. Funkce užitku, která popisuje Isaacovy preference pro svazky jablek a banánů, je funkce U(A,B). Jaké jsou však Isaacovy konkrétní preference pro svazky jablek a banánů? Předpokládejme, že Isaac má poměrně standardní preference pro jablka a banány, které vedou k našim typickým indiferenčním křivkám: Dává přednost většímu množství před menším a má rád rozmanitost. Funkce užitku, která reprezentuje tyto preference, by mohla vypadat takto:
U(A,B) = AB
Pokud jsou jablka a banány v Isaacových preferencích dokonalými komplementy, funkce užitku by vypadala nějak takto:
U(A,B) = MIN,
kde funkce MIN jednoduše přiřazuje menší z obou čísel jako hodnotu funkce.
Jsou-li jablka a banány dokonalými substituty, funkce užitku je aditivní a vypadala by nějak takto:
U(A,B) = A + B
Třída funkcí užitku známá jako Cobb-Douglasovy funkce užitku se v ekonomii velmi často používá ze dvou důvodů:
1. Funkce užitku se nazývá Cobb-Douglasova funkce užitku. Reprezentují „dobře zvládnuté“ preference, jako například více je lépe a preference rozmanitosti
2. Jsou velmi flexibilní a lze je velmi snadno upravit tak, aby odpovídaly reálným datům.
Cobb-Douglasovy funkce užitku mají tento tvar:
U(A,B) = AαBβ
Protože kladné monotónní transformace reprezentují stejné preference, lze jednu takovou transformaci použít k nastavení α + β = 1 , což, jak později uvidíme, je výhodná podmínka, která zjednodušuje některé matematické operace v problému volby spotřebitele.
Dalším způsobem, jak užitečně transformovat funkci užitku, je vzít přirozený logaritmus funkce, čímž vznikne nová funkce, která vypadá takto:
U(A,B) = αln(A) + βln(B)
Pro odvození této rovnice stačí použít pravidla přirozených logaritmů. . Je důležité mít zde na paměti úroveň abstrakce. Obvykle nemůžeme vytvořit konkrétní funkce užitku, které by přesně popisovaly individuální preference. Pravděpodobně nikdo z nás by nedokázal popsat své vlastní preference jedinou rovnicí. Ale pokud mají spotřebitelé obecně preference, které se řídí našimi základními předpoklady, můžeme docela dobře najít funkce užitku, které odpovídají údajům o reálné spotřebě. Důkazy o tom uvidíme později v průběhu kurzu.
Tabulka 2.1 shrnuje preference a funkce užitku popsané v této části.
|
Tabulka 2. Preference a funkce užitku.1 Typy preferencí a funkce užitku, které je reprezentují |
||
|
PREFERENCE |
UŽITEK. FUNKCE |
TIP UTILITY FUNKCE |
|
Láska k rozmanitosti nebo „dobře se chovat“ |
U(A,B) = AB |
Cobb-Douglas |
|
Láska k rozmanitosti nebo „dobře se chovající“ |
U(A,B) = AαBβ |
Cobb-Douglas |
|
Láska k rozmanitosti nebo „dobře se chovat“ |
U(A,B) = αln(A) + βln(B) |
Přirozený Log Cobb-Douglas |
|
Dokonalé doplňky |
U(A,B) = MIN |
Min funkce |
|
Dokonalé substituty |
U(A,B) = A + B |
Aditivní |
2.3 Vztahování funkcí užitku a map indiferenčních křivek
LO3: Vysvětlete, jak z funkce užitku odvodit indiferenční křivku
Indiferenční křivky a funkce užitku spolu přímo souvisejí. Protože indiferenční křivky znázorňují preference graficky a užitkové funkce je znázorňují matematicky, vyplývá z toho, že indiferenční křivky lze odvodit z užitkových funkcí.
U jednovariantních funkcí je závislá proměnná vynesena na svislou osu a nezávislá proměnná na vodorovnou osu, podobně jako graf y=f(x). Naproti tomu grafy dvourozměrných funkcí jsou trojrozměrné, například U=U(A,B). Obrázek 2.1 ukazuje graf funkce U=A^\frac{1}{2}B^\frac{1}{2}. Trojrozměrné grafy jsou užitečné pro pochopení toho, jak užitek roste s rostoucí spotřebou A i B.
Obrázek 2.1 U=A^\frac{1}{2}B^\frac{1}{2}
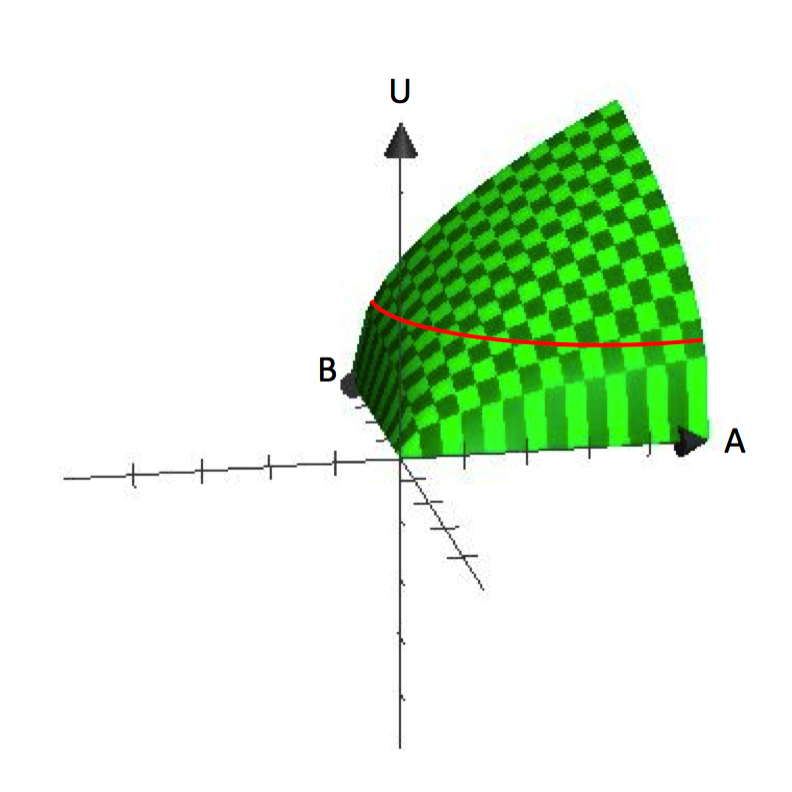
Obrázek 2.1 jasně ukazuje předpoklad, že spotřebitelé preferují rozmanitost. Každý svazek, který obsahuje určité množství A a B, představuje bod na povrchu. Svislá výška plochy představuje úroveň užitku. Zvýšením A i B může spotřebitel dosáhnout vyšších bodů na povrchu.
Kde se tedy berou indiferenční křivky? Připomeňme si, že indiferenční křivka je soubor všech balíčků, ke kterým je spotřebitel lhostejný, s ohledem na to, který z nich má spotřebovávat. Matematicky je to ekvivalentní tvrzení, že všechny balíčky po dosazení do funkce užitku vracejí stejnou funkční hodnotu. Pokud tedy stanovíme hodnotu užitku, Ū, a najdeme všechny svazky A a B, které tuto hodnotu generují, definujeme indiferenční křivku. Všimněte si, že to je ekvivalentní nalezení všech svazků, které dostanou spotřebitele do stejné výšky na trojrozměrném povrchu na obrázku 2.1.
Indiferenční křivky jsou znázorněním výšky (úrovně užitku) na rovném povrchu. V tomto smyslu jsou analogické obrysové čáře na topografické mapě. Převedeme-li trojrozměrný graf zpět do dvourozměrného prostoru – do prostoru A, B – můžeme zobrazit obrysové čáry/indiferenční křivky, které představují různé nadmořské výšky nebo úrovně užitku. Již z grafu na obrázku 2.1 vidíte, jak tato funkce užitku dává indiferenční křivky, které jsou „skloněné“ nebo konkávní k počátku.
Indiferenční křivky tedy vyplývají přímo z funkce užitku a jsou užitečným způsobem, jak znázornit funkce užitku ve dvourozměrném grafu.
2.4 Zjištění mezního užitku a mezní míry substituce
LO4: Odvoďte mezní užitek a MRS pro typické funkce užitku.
Mezní užitek je dodatečný užitek, který spotřebitel získá ze spotřeby jedné dodatečné jednotky zboží. Matematicky jej vyjadřujeme takto:
MU_{a}=\frac{\Delta \cup }{\Delta A}
neboli změna užitku ze změny množství spotřebovaného A, kde Δ představuje změnu hodnoty zboží. Takže,
MU_{a}=\frac{\Delta \cup }{\Delta A}=\frac{\cup (A+\Delta A,B)-U(A,B)}{\Delta A}
Všimněte si, že když zkoumáme mezní užitek ze spotřeby A, držíme B konstantní.
Pomocí kalkulu je mezní užitek totožný s parciální derivací funkce užitku vzhledem k A:
MU_{A}\frac{\parciální U(A,B)}{\parciální A}
Považme spotřebitele, který si sedne k jídlu ze salátu a pizzy. Předpokládejme, že množství salátu ponecháme konstantní – například jeden přílohový salát k večeři. Nyní zvětšeme počet kousků pizzy předpokládejme, že s 1kouskem je užitek 10, se 2 je 18, se 3je 24 a se 4 je 28. To znamená, že s 1 kouskem pizzy je užitek 10, se 2 je 18, se 3 je 24 a se 4 je 28. Vynesme tato čísla do grafu, který má užitek na svislé ose a pizzu na vodorovné ose (obrázek 2.2).
Obrázek 2.2: Graf a tabulka klesajícího mezního užitku
|
Kousky pizzy |
Užitek |
Mezní užitek Užitkové |
|
1 |
10 |
|
|
2 |
18 |
8 |
|
3 |
24 |
6 |
|
4 |
28 |
4 |
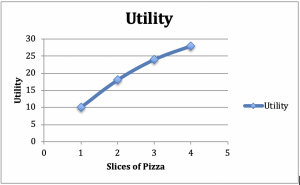
Z kladného sklonu grafu, vidíme nárůst užitku z dalších kousků pizzy. Z konkávního tvaru grafu můžeme vidět další společný jev:
To, že se dodatečný užitek s každým dalším kouskem pizzy zmenšuje, se nazývá princip klesajícího mezního užitku. Tento princip platí pro dobře chápané preference, kdy jsou preferovány smíšené balíčky.
Marginální míra substituce (MRS) je množství jednoho zboží, kterého je spotřebitel ochoten se vzdát, aby získal další jednotku jiného zboží. Proto je to totéž co sklon indiferenční křivky – protože udržujeme úroveň uspokojení konstantní, zůstáváme na stejné indiferenční křivce, jen se po ní pohybujeme, když vyměňujeme jedno zboží za druhé. Kolik z jednoho jste ochotni vyměnit za jeden další kus jiného závisí na mezním užitku z každého z nich.
Podle našeho předchozího příkladu, pokud se spotřebou jednoho salátu navíc zvýší váš užitek o 10, pak byste se při současné spotřebě 4 kousků pizzy mohli vzdát 2 kousků pizzy a dostat se z 28 na 18 užitků. O 10 více užitku ze salátu a o 10 méně užitku vzdáním se 2 plátků pizzy ponechává celkový užitek beze změny – musíme se tedy stále nacházet na stejné indiferenční křivce. Při pohybu po indiferenční křivce musíme jet po jejím sklonu, to znamená, že se musíme vzdát zboží na svislé ose za více zboží na vodorovné ose, což přináší záporný nárůst při kladném průběhu.
Můžeme přejít přímo od mezního užitku k MRS, když si uvědomíme souvislost mezi těmito dvěma pojmy. V našem případě je pro funkci užitku U=U(A,B) , MRS reprezentována jako:
MRS=-\frac{MU_{A}}{MU_{B}}
Všimněte si, že při substituci můžeme rovnici zjednodušit:
MRS=-\frac{MU_{A}}{MU_{B}}=-\frac{\frac{\Delta U}{\Delta A}}{\frac{\Delta U}{\Delta B}}=-\frac{\Delta B}{\Delta A}
Při dosazení do výpočtu to znamená:
MRS=-\frac{\frac{\část U(A,B)}{\část A}}{\frac{\část U(A,B)}{\část B}}
2.5 Politická otázka
V modulu 1 jsme určili, že příslušné spotřebitelské rozhodnutí mezi větším počtem ujetých kilometrů a jinou spotřebou pravděpodobně odpovídá standardním předpokladům o spotřebitelské volbě. Proto je použití Cobb-Douglasovy funkce užitku pro reprezentaci spotřebitele, který rád jezdí autem i spotřebovává jiné statky a který je vnímá jako kompromis (peníze utracené za benzín jsou peníze neutracené za jiné spotřební statky), dobrou volbou. Její výhodou je také to, že odpovídá předpokladům a je flexibilní:
U(MD,C)=MD^{a}C^{\beta } ,
kde MD = ujeté kilometry a C = ostatní spotřeba.
Ve skutečnosti lze samotnou funkci vzít na reálná data, kde lze parametry a odhadnout pro tento trh, trh ujetých kilometrů ve spotřebitelově autě.
Obrázek 2.3 Graf indiferenčních křivek pro příklad politiky
Zkoumání otázek politiky:
1 . Byly by v tomto příkladu vhodnější jiné typy preferencí?
2. Co by muselo platit pro dokonalé komplementy, aby byly vhodným typem preferencí pro analýzu této politiky?
Co by muselo platit pro dokonalé substituty?
3. Vzhledem k tomu, že uvažujeme o „typickém“ spotřebiteli, který řídí, je vhodné zvolit „typickou“ funkci užitku?
4. Jenom hádáme, nebo máme nějaký teoretický základ, který podporuje naši volbu „dobře vychovaných“ preferencí nebo Cobb-Douglasovy funkce užitku?
SHRNUTÍ
Přehled: Témata a související výsledky učení
2.1 Funkce užitku
LO 2.1: Popište funkci užitku
2.2 Funkce užitku a typické preference
LO 2.2: Identifikovat funkce užitku na základě typických preferencí, které reprezentují
2.3 Vztah mezi funkcemi užitku a mapami indiferenčních křivek
LO 2.3: Vysvětlit, jak z funkce užitku odvodit indiferenční křivku
2.4 Zjištění mezního užitku a mezní míry substituce
LO 2.4: Odvodit mezní užitek a MRS pro typické funkce užitku
2.5: Odvodit mezní užitek a MRS pro typické funkce užitku. Politická otázka
Učte se: Klíčové pojmy a grafy
Bi-variačních funkcí
Kardinální
Konkávní přímka
Klesající mezní užitek
Funkce
Mezní míra substituce (MRS)
Mezní užitek
.
Ordinální
Jednotlivé funkce
Užitek
Užitečnost
Funkce užitku
Grafy
3D funkce užitku a obrysová čára
Rovnice
Kobbova-Douglas
Dokonalé doplňky
Dokonalé substituty
.