MezopotámieEdit
V období 2700-2300 př. n. l. se poprvé objevil sumerský abakus, tabulka po sobě jdoucích sloupců, která vymezovala postupné řády jejich sexagesimální číselné soustavy.
Někteří badatelé poukazují na znak v babylonském klínopise, který mohl být odvozen od zobrazení abaku. Starobabylónští badatelé, jako například Carruccio, se domnívají, že starobabylóňané „možná používali abakus pro operace sčítání a odčítání; toto primitivní zařízení se však ukázalo jako obtížně použitelné pro složitější výpočty“.
EgyptskýEdit
O používání abaku ve starém Egyptě se zmiňuje řecký historik Hérodotos, který píše, že Egypťané manipulovali s kamínky zprava doleva, což je opačný směr než u řecké metody zleva doprava. Archeologové našli starověké kotouče různých velikostí, o nichž se předpokládá, že se používaly jako počítadla. Nástěnná vyobrazení tohoto nástroje však nebyla objevena.
PeršanéEdit
V době Achaimenovské říše, kolem roku 600 př. n. l., začali Peršané poprvé používat abakus. Za Parthské, Sásánovské a Íránské říše se učenci soustředili na výměnu znalostí a vynálezů s okolními zeměmi – Indií, Čínou a Římskou říší, kdy se předpokládá, že byl vyvážen do dalších zemí.
ŘeckáEdit
Nejstarší archeologické doklady o používání řeckého abakusu pocházejí z 5. století př. n. l.. Také Démosthenés (384 př. n. l. – 322 př. n. l.) hovořil o nutnosti používat oblázky pro výpočty příliš složité pro hlavu. V jedné Alexiově hře ze 4. století př. n. l. je zmínka o počítadle a kamíncích pro počítání a Diogenés i Polybios se zmiňují o mužích, kteří někdy stáli za více a někdy za méně, podobně jako kamínky na počítadle. Řecký abakus byl dřevěný nebo mramorový stůl předem osazený malými dřevěnými nebo kovovými počítadly pro matematické výpočty. Tento řecký abakus se používal v achaimenovské Persii, v etruské civilizaci, ve starověkém Římě a až do Francouzské revoluce v západním křesťanském světě.
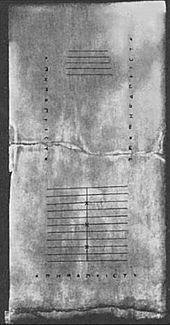
Tabulka nalezená na řeckém ostrově Salamína v roce 1846 n. l. (Salamínská tabulka) pochází z roku 300 př. n. l., což z ní činí nejstarší dosud objevenou počítací tabulku. Jedná se o desku z bílého mramoru dlouhou 149 cm (59 palců), širokou 75 cm (30 palců) a silnou 4,5 cm (2 palce), na níž je 5 skupin značek. Uprostřed desky je soubor 5 rovnoběžných čar rovnoměrně rozdělených svislou čarou, zakončený půlkruhem v průsečíku nejspodnější vodorovné čáry a jediné svislé čáry. Pod těmito liniemi je široký prostor, který je rozdělen vodorovnou prasklinou. Pod touto trhlinou je další skupina jedenácti rovnoběžných čar, opět rozdělených na dvě části kolmou čarou, ale s půlkruhem v horní části průsečíku; třetí, šestá a devátá z těchto čar jsou v místě průsečíku se svislou čarou označeny křížkem. Z tohoto časového rámce pochází také Dariova váza vykopaná v roce 1851. Byla pokryta obrázky včetně „pokladníka“, který v jedné ruce drží voskovou tabulku a druhou rukou manipuluje s počítadly na stole.
ChineseEdit

| Abakus | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tradiční čínština | 算盤 | |||||||||||||||
| Zjednodušená čínština | 算盘 | |||||||||||||||
| Literární jazyk význam | „počítací zásobník“ | |||||||||||||||
| Přepis | Standardní mandarínština | Hanyu Pinyin | IPA | Yue: Kantonština | Jalská romanizace | Jyutping | IPA | Jižní Min | Hokkien POJ | Tâi-lô | ||||||
Nejstarší známé písemné doklady o čínském počítadle pocházejí z 2. století před naším letopočtem.
Čínské počítadlo, známé jako suanpan (算盤/算盘, doslova „počítací tác“), je obvykle 20 cm vysoké a v závislosti na obsluze je různě široké. Obvykle má více než sedm tyčí. V horním patře jsou na každé tyči dvě kuličky a ve spodním patře po pěti kuličkách. Korálky jsou obvykle zaoblené a vyrobené z tvrdého dřeva. Korálky se počítají pohybem nahoru nebo dolů směrem k trámu; korálky posunuté směrem k trámu se počítají, zatímco ty, které se od něj vzdalují, se nepočítají. Jeden z horních korálků je 5, zatímco jeden ze spodních korálků je 1. Každá tyčinka má pod sebou číslo, které udává hodnotu místa. suanpan lze okamžitě vrátit do výchozí polohy rychlým pohybem podél vodorovné osy, aby se všechny korálky roztočily směrem od vodorovného paprsku ve středu.
Předloha čínského počítadla se objevila za dynastie Chan a korálky jsou oválné. Za dynastie Song a dříve se používal počítadlo typu 1:4 neboli počítadlo se čtyřmi korálky podobné modernímu počítadlu včetně tvaru korálků, které je běžně známé jako počítadlo v japonském stylu.
Na počátku dynastie Ming se počítadlo začalo objevovat v podobě počítadla 1:5. V době, kdy se počítadlo začalo používat jako počítadlo, se počítadlo začalo používat jako počítadlo. Horní patro mělo jeden korálek a spodní pět korálků.
Na konci dynastie Ming se objevily styly abakusů v podobě 2:5. Horní patro mělo dva korálky a spodní pět korálků.
Pro Suanpan byly vymyšleny různé výpočetní techniky umožňující efektivní výpočty. V současné době existují školy, které učí studenty, jak jej používat.
Na dlouhém svitku Podél řeky během svátku Qingming, který namaloval Zhang Zeduan za dynastie Song (960-1297), je suanpan jasně vidět vedle účetní knihy a lékařských receptů na pultu lékárny (Feibao).
Podobnost římského abakusu s čínským naznačuje, že jeden mohl inspirovat druhý, protože existují určité důkazy o obchodních vztazích mezi Římskou říší a Čínou. Žádnou přímou souvislost však nelze prokázat a podobnost počítadel může být náhodná, obě nakonec vznikla počítáním s pěti prsty na ruce. Zatímco římský model (stejně jako většina moderních korejských a japonských) má 4 plus 1 korálek na desetinné místo, standardní suanpan má 5 plus 2. To mimochodem umožňuje použití šestnáctkové číselné soustavy (nebo jakéhokoli základu až do 18), která mohla být použita pro tradiční čínské míry hmotnosti. (Místo na drátcích jako u čínských, korejských a japonských modelů se kuličky římského modelu pohybují v drážkách, což pravděpodobně značně zpomaluje aritmetické výpočty.
Dalším možným zdrojem suanpanu jsou čínské počítací tyče, které pracovaly s desítkovou soustavou, ale postrádaly koncept nuly jako držitele místa. Nula byla Číňanům pravděpodobně představena za dynastie Tchang (618-907), kdy jim cesty po Indickém oceánu a Blízkém východě mohly zprostředkovat přímý kontakt s Indií, což jim umožnilo osvojit si koncept nuly a desetinné čárky od indických obchodníků a matematiků.
RomanEdit

Obvyklý způsob počítání ve starém Římě, stejně jako v Řecku, spočíval v pohybu počítadel na hladkém stole. Původně se používaly oblázky (calculi). Později a ve středověké Evropě se vyráběly jetony. Vyznačené čáry označovaly jednotky, pětky, desítky atd. jako v římské číselné soustavě. Tento systém „odlévání počítadel“ pokračoval i v pozdní římské říši a ve středověké Evropě a v omezené míře se používal až do devatenáctého století. Díky tomu, že papež Sylvestr II. počítadlo s úpravami znovu zavedl, začalo se v Evropě během 11. století opět hojně používat Toto počítadlo používalo na rozdíl od tradičních římských počítacích desek korálky na drátcích, což znamenalo, že počítadlo bylo možné používat mnohem rychleji.
Horacius píše v 1. století př. n. l. o voskovém abaku, desce pokryté tenkou vrstvou černého vosku, na kterou se pomocí rydla zapisovaly sloupce a číslice.
Jeden příklad archeologického dokladu římského abaku, který je zde zobrazen v rekonstrukci, pochází z 1. století n. l. V tomto případě se jedná o desku pokrytou tenkou vrstvou černého vosku. Má osm dlouhých drážek, z nichž každá obsahuje až pět korálků, a osm kratších drážek, z nichž každá má buď jeden, nebo žádný korálek. Drážka označená I označuje jednotky, X desítky a tak dále až do milionů. Korálky v kratších drážkách označují pětky – pět jednotek, pět desítek atd., v podstatě ve dvojkové kódované desítkové soustavě, příbuzné římským číslicím. Krátké drážky vpravo mohly sloužit k označení římských „uncí“ (tj. zlomků).
IndickýEdit
Abhidharmakośabhāṣya Vasubandhu (316-396), sanskrtské dílo o buddhistické filozofii, uvádí, že filosof Vasumitra z druhého století n. l. řekl, že „položení knotu (sanskrtsky vartikā) na číslo jedna (ekāṅka) znamená, že je to jednička, zatímco položení knotu na číslo sto znamená, že se nazývá sto, a na číslo tisíc znamená, že je to tisíc“. Není jasné, jak přesně mohlo toto uspořádání vypadat. Kolem 5. století již indičtí úředníci nacházeli nové způsoby, jak zaznamenávat obsah abaku. V hinduistických textech se pro označení prázdného sloupce na abaku používal termín śūnya (nula).
JapaneseEdit

V japonštině se počítadlo nazývá soroban (算盤, そろばん, doslova „Počítací tác“), dovezené z Číny ve 14. století. Dělnická třída jej pravděpodobně začala používat o sto či více let dříve než vládnoucí třída, protože třídní struktura neumožňovala, aby zařízení používaná nižší třídou převzala nebo používala vládnoucí třída. Abakus 1/4, který odstraňuje zřídka používaný druhý a pátý korálek, se stal populárním ve 40. letech 19. století.
Dnešní japonský abakus je typu 1:4, čtyřkorálkový abakus byl zaveden z Číny v éře Muromači. Přebírá tvar horního patra s jedním korálkem a spodního se čtyřmi korálky. Horní korálek na horním patře byl roven pěti a spodní je roven jedné jako u čínského nebo korejského abaku a lze vyjádřit desetinné číslo, takže abakus je navržen jako jeden čtyřkový abakus. Korálky jsou vždy ve tvaru kosočtverce. Místo metody dělení se obvykle používá dělení kvocientem; zároveň, aby se číslice násobení a dělení důsledně používaly, se používá násobení dělením. Později se v Japonsku objevil abakus 3:5 s názvem 天三算盤, který je nyní ve sbírce Ize Rongji z vesnice Šanši ve městě Jamagata. Existovaly také abaky typu 2:5.
S rozšířením čtyřkuličkových abaků se japonské abaky běžně používají i ve světě. Na různých místech se objevují také vylepšené japonské abakusy. Jedním z japonských abaků vyráběných v Číně je abakus s hliníkovým rámem z plastových kuliček. Pilník je vedle čtyř kuliček a tlačítka „clearing“, stisknutím tlačítka clearing okamžitě nastavíte horní kuličku do horní polohy, spodní kulička se vytočí do dolní polohy, okamžitě clearing, snadné použití.
Abakus se v Japonsku vyrábí dodnes, i když se rozšířily, jsou praktické a cenově dostupné kapesní elektronické kalkulačky. Používání sorobanu se stále vyučuje na japonských základních školách v rámci matematiky, především jako pomůcka pro rychlejší mentální výpočty. Pomocí vizuální představy sorobanu lze dospět k odpovědi ve stejném čase, nebo dokonce rychleji, než je to možné s fyzickým přístrojem.
KoreanEdit
Čínský abakus se z Číny přestěhoval do Koreje kolem roku 1400 našeho letopočtu. Korejci mu říkají jupan (주판), supan (수판) nebo jusan (주산). čtyřkorálkový abakus( 1:4 ) byl do Koreje zaveden dynastií Goryeo z Číny za dynastie Song, později byl do Koreje z Číny za dynastie Ming zaveden abakus s pěti korálky (5:1).
IndiániEdit


Některé prameny uvádějí používání počítadla zvaného nepohualtzintzin ve starověké aztécké kultuře. Tento mezoamerický abakus používal pětimístný systém se základem 20. Slovo nepōhualtzintzin pochází z nahuatlu a je tvořeno kořeny; ne – osobní -; pōhual nebo pōhualli – účet -; a tzintzin – malé podobné prvky. Jeho úplný význam byl převzat jako: počítání s malými podobnými prvky někým. Jeho používání se v Kalmecu učili temalpouhqueh , což byli studenti určení k pořizování účtů oblohy, již od dětství.
Nepōhualtzintzin se dělil na dvě hlavní části oddělené pruhem nebo mezivrstvou. V levé části byly čtyři korálky, které mají v první řadě jednotkové hodnoty (1, 2, 3 a 4), a v pravé části jsou tři korálky s hodnotami 5, 10 a 15 v uvedeném pořadí. Abychom se dozvěděli hodnotu příslušných korálků horních řad, stačí vynásobit 20 (u každé řady) hodnotu příslušného účtu v první řadě.
Celkem bylo 13 řad se 7 korálky v každé z nich, což tvořilo 91 korálků v každém Nepōhualtzintzinu. To bylo základní číslo k pochopení, 7 krát 13, úzký vztah pojatý mezi přírodními jevy, podsvětím a nebeskými cykly. Jeden Nepōhualtzintzin (91) představoval počet dní, které trvá jedno roční období, dva Nepōhualtzitzin (182) je počet dní cyklu obilí, od jeho zasetí po sklizeň, tři Nepōhualtzintzin (273) je počet dní těhotenství dítěte a čtyři Nepōhualtzintzin (364) dokončovaly cyklus a přibližně rok (chybělo 11/4 dne). Při převodu do moderní počítačové aritmetiky se Nepōhualtzintzin rovnal hodnosti od 10 do 18 v pohyblivé řádové čárce, která počítala hvězdné i nekonečně malé částky s absolutní přesností, což znamenalo, že nebylo povoleno žádné zaokrouhlování.
O znovuobjevení Nepōhualtzintzinu se zasloužil mexický inženýr David Esparza Hidalgo, který na svých toulkách po Mexiku nalezl rozmanité rytiny a malby tohoto nástroje a rekonstruoval několik z nich zhotovených ze zlata, nefritu, inkrustací mušlí atd. Byly nalezeny také velmi staré nephualtzintziny připisované olmécké kultuře, a dokonce i některé náramky mayského původu, stejně jako rozmanité formy a materiály v jiných kulturách.
George I. Sanchez, „Arithmetic in Maya“, Austin-Texas, 1961 našel na poloostrově Yucatán další abakus se základem 5 a základem 4, který počítal i kalendářní údaje. Jednalo se o prstový abakus, na jedné straně se používaly hodnoty 0, 1, 2, 3 a 4, na druhé straně 0, 1, 2 a 3. V tomto případě se jednalo o abakus, na kterém se používaly hodnoty 0, 1, 2 a 3. Všimněte si použití nuly na začátku a na konci obou cyklů. Sanchez spolupracoval se Sylvanusem Morleyem, známým mayistou.
Quipu Inků byl systém barevných uzlíkových šňůr, který se používal k zaznamenávání číselných údajů, podobně jako pokročilé sčítací tyče – nepoužíval se však k provádění výpočtů. Výpočty se prováděly pomocí yupany (kečuánsky „počítací nástroj“; viz obrázek), která se používala i po dobytí Peru. Princip fungování yupany není znám, ale v roce 2001 navrhl vysvětlení matematického základu těchto nástrojů italský matematik Nicolino De Pasquale. Porovnáním podoby několika yupan vědci zjistili, že výpočty byly založeny na použití Fibonacciho posloupnosti 1, 1, 2, 3, 5 a mocnin 10, 20 a 40 jako hodnot umístění jednotlivých polí v nástroji. Použití Fibonacciho posloupnosti by udrželo počet zrn v rámci jednoho pole na minimu.
Ruské počítadlo

Ruské počítadlo, šoty (rusky: счёты, množné číslo z rus: счёт, počítání), má obvykle jedno šikmé patro s deseti korálky na každém drátu (s výjimkou jednoho drátu, obvykle umístěného v blízkosti uživatele, se čtyřmi korálky pro čtvrtinové zlomky). Starší modely mají ještě jeden drát se čtyřmi korálky pro čtvrtkopějky, které se razily do roku 1916. Ruské počítadlo se často používá vertikálně, s jednotlivými dráty zleva doprava jako řádky v knize. Drátky jsou obvykle ohnuté tak, aby se uprostřed vypoukly nahoru, aby korálky zůstaly přichycené na jedné ze dvou stran. Vyčistí se, když se všechny korálky posunou doprava. Při manipulaci se korálky posouvají doleva. Pro snadnější přehled jsou prostřední dva korálky na každém drátu (5. a 6. korálek) obvykle jiné barvy než ostatních osm korálků. Stejně tak může mít jinou barvu levý korálek na tisíci drátech (a milionový drát, pokud je přítomen).
Jako jednoduchý, levný a spolehlivý přístroj se ruské počítadlo používalo ve všech obchodech a na trzích po celém bývalém Sovětském svazu a jeho používání se vyučovalo na většině škol až do 90. let 20. století. V Rusku je nenahradil ani vynález mechanického kalkulátoru, Odhnerova aritmometru, z roku 1874; podle Jakova Perelmana bylo dokonce známo, že někteří obchodníci, kteří se pokoušeli dovážet tyto přístroje do ruského impéria, to vzdali a v zoufalství odešli poté, co jim ukázali práci zkušeného operátora abaku. Stejně tak masová výroba Felixových aritmometrů od roku 1924 nijak výrazně neomezila jejich používání v Sovětském svazu. Ruské počítací stroje začaly ztrácet na popularitě až poté, co se v Sovětském svazu v roce 1974 začala masová výroba mikropočítačů. Dnes je považován za archaismus a nahrazen kapesní kalkulačkou.
Ruské počítadlo přivezl do Francie kolem roku 1820 matematik Jean-Victor Poncelet, který sloužil v Napoleonově armádě a byl válečným zajatcem v Rusku. V západní Evropě se abakus přestal používat v 16. století s nástupem desítkové notace a algoritmických metod. Pro Ponceletovy francouzské současníky to bylo něco nového. Poncelet ho nepoužíval k žádnému praktickému účelu, ale jako učební a demonstrační pomůcku. Turci a Arméni také používali počítadla podobná ruským schotům. Turci ho nazývali coulba a Arméni choreb.
.